Lois du mouvement de Newton - Définition

Problèmes et limites

Univers absolu

Newton avait postulé : il existe un espace et un temps absolu.

En fait, on pouvait étendre à toute une classe de référentiels dits « inertiels » la notion d'espace absolu : quête sans fin, mais de plus en plus précise. Si aucun référentiel usuel n'est parfaitement inertiel, on peut du moins prouver qu'ils existent. Mais Newton a eu tort de ne pas croire entièrement Galilée qui défendait l'équivalence entre un référentiel et un autre évoluant à vitesse constante par rapport au premier.

Par contre, Newton se méfiait du temps absolu : il savait qu'en changeant l'échelle de temps, l'expression de son PFD changeait. Il l'a même savamment utilisé. Mais évidemment, il fallait prendre une décision : quelle échelle de temps choisir ? Ce qui paraissait le plus simple était la fameuse loi de Kepler. Et tout était cohérent.

Les notions de temps relatif, de finitude des vitesses, de synchronisation et de transport du temps allaient nécessiter encore beaucoup de découvertes avant d'être entrevues. Il a donc opté pour le temps dynamique absolu et édicté : le temps absolu s'écoule uniformément. C'est cette variable t qui intervient quand on écrit

,

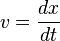
puis

,

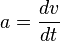
et donc :

.

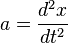
Ce temps absolu est généralement admis tant qu'on n'emploie pas la relativité restreinte. Mais il constitue néanmoins une hypothèse philosophique forte qui a été régulièrement discutée par Leibniz notamment qui disait :

« J'ai marqué plus d'une fois que je tenais l'espace pour quelque chose de purement relatif, comme le temps ; pour un ordre de coexistences comme le temps est un ordre de successions… »

Limites relativistes

Une des grandes difficultés des théories de Newton, mise à jour dès le XVII^e siècle est la notion d'action instantanée à distance. Newton lui-même était gêné par cette supposition présente tout aussi bien dans sa théorie de la gravitation que dans sa troisième loi.
Plus tard au cours du XVII^e siècle un certain nombre de difficultés, concernant l'électromagnétisme notamment, indiquèrent également que les principes de Newton ne pouvaient pas rendre compte en l'état de tous les problèmes mécaniques ou cinématiques.

La relativité restreinte démontre aujourd'hui qu'aucune interaction ne se propage plus vite que la vitesse de la lumière et remet donc définitivement en cause les interactions instantanées. De plus elle montre que pour des objets dont la vitesse est proche de celle de la lumière, les lois de Newton ne sont plus une bonne approximation. En fait, les formules de la relativité restreinte permettent de considérer la physique newtonienne comme une approximation en supposant c infinie.

Ainsi les lois de Newton ne sont pas réfutées par Einstein ; au contraire, la relativité permet de justifier les équations de Newton dans les cas de faibles vitesses en la rendant démontrable à partir d'une théorie plus générale qui l'englobe.

D'autre part même en relativité restreinte, les forces respectent toujours un théorème de la quantité de mouvement mais adapté, faisant apparaître le facteur de Lorentz. Le théorème de la quantité de mouvement est donc un théorème très puissant, puisqu'il permet de déduire les lois de Newton dans le cas où les faibles vitesses le permettent. Dans le cas contraire il s'inscrit dans les résultats de la relativité restreinte.

Il serait bien sûr absurde de dire que les lois de Newton sont fausses. La chute d'un corps sur Terre est un cas où les corrections apportées par la relativité sont minimes, comme pour la plupart des applications quotidiennes de la mécanique classique.

En revanche, une situation où les résultats sont radicalement modifiés est celle, par exemple, des accélérateurs de particules du CERN. L'énergie cinétique apportée à une particule de charge q par une tension V vaut q V. Avec le TeraVolt (1 000 milliards de volts) du CERN, on trouve classiquement pour un électron une vitesse 2 000 000 fois supérieure à la vitesse de la lumière. La vitesse réelle, calculée dans le cadre relativiste est celle de la lumière diminuée de quelques microns/seconde. Il est donc essentiel de bien distinguer les situations où les lois de Newton sont valables de celles où elles ne sont plus utilisables.

Limites quantiques

La mécanique Newtonienne étudie surtout les systèmes macro-physiques. Dans ce contexte, l'espace et l'énergie sont implicitement considérés comme étant continus. Or, le monde de la mécanique quantique est celui des systèmes micro-physiques, pour lesquels ces concepts sont quantifiés. La mécanique Newtonienne s'appuie notamment sur le concept de force, sachant que la force dérive d'un potentiel (pour un système mécanique isolé). Toutefois, pour les systèmes micro-physiques (relevant de la mécanique quantique), la notion de force ne peut pas être définie puisque l'énergie potentielle comme les coordonnées d'espace sont quantifiées. En effet, en mathématique, la dérivée d'une fonction discontinue n'est pas définie. La mécanique de Newton trouve donc ses limites pour l'étude des systèmes micro-physiques, puisque l'hypothèse implicite basée sur un espace et une énergie continus est mise à mal pour ces systèmes.