Lois du mouvement de Newton - Définition

Deuxième loi de Newton ou principe fondamental de la dynamique de translation

Énoncé

La deuxième loi de Newton (ou principe fondamental de la dynamique en translation (PFDT) - parfois appelée relation fondamentale de la dynamique ou (RFD) s'énonce ainsi : Soit un corps de masse m (constante) : l'accélération subie par ce corps dans un référentiel galiléen est proportionnelle à la résultante des forces qu'il subit, et inversement proportionnelle à sa masse m.

Ceci est souvent récapitulé dans l'équation :

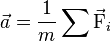
— ou —

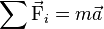
où

• désigne les forces extérieures exercées sur l'objet,
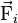
• m est sa masse, et
• correspond à l'accélération de son centre d'inertie G.

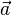
Enseignement de la deuxième loi de Newton

Les étudiants éprouvent de grandes difficultés pour utiliser les lois de Newton telles qu’elles sont traditionnellement énoncées et ce n’est pas sans raison. En effet les forces semblent s’exercer comme si elles existaient en elles-mêmes, ex abrupto. Proposons donc une nouvelle formulation de la loi en l’accompagnant de son mode opératoire afin que chacun puisse l’appliquer rationnellement, c’est-à-dire en argumentant.

Dans un repère galiléen la somme des forces que les objets extérieurs à l’objet B exercent sur B est égale au produit de la masse m_B de B par l'accélération de B :

.

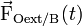
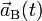
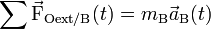
L’écriture fait apparaître que les forces et l’accélération varient au cours du temps, alors que la masse de l’objet est considérée comme constante dans le domaine de validité considéré et que les vitesses des objets macroscopiques sont faibles par rapport à la vitesse de la lumière.

Dans les problèmes qui visent à décrire le mouvement d’un objet B lorsqu’il est immuable et représentable par un point (ce qu’on appelle le modèle du « point matériel »), les procédures d’utilisation sont les suivantes :

• Sélectionner par la pensée l’objet B dont on veut décrire le mouvement.
• Répertorier tous les objets qui lui sont extérieurs et qui exercent une force « notable » sur B. Pour y parvenir il est indispensable de connaître les ordres de grandeur des différentes interactions entre les objets matériels en présence afin de les hiérarchiser ; seules les plus intenses interviennent dans la modélisation de la situation où se pose le problème à résoudre.

Retour sur le principe d'inertie

Pour un corps soumis à une résultante des forces nulle on retrouve bien la première loi de Newton, c’est-à-dire un mouvement rectiligne uniforme. En première analyse, on peut se demander quelle est l'utilité de la première loi puisqu'elle semble être une conséquence de la deuxième. En réalité, dans l'énoncé de Newton, il n'en est rien car la première loi n'est pas présentée comme un cas particulier de la deuxième mais comme une condition suffisante à l'application de cette dernière. En effet, énoncer la première loi, c'est affirmer l'existence des référentiels galiléens. Cela constitue un postulat extrêmement fort qui permet, dans les exposés modernes de la mécanique classique, de définir les repères galiléens qui sont les seuls repères dans lesquels la seconde loi est valide. En l'absence de la première loi, la seconde loi est inapplicable puisqu'on ne peut pas définir son domaine de validité. Par conséquent, l'ordre logique dans lequel les lois sont énoncées n'est pas le fruit du hasard mais bien celui d'une construction intellectuelle cohérente.