Lois de Kepler - Définition

Quand ces lois s'appliquent-elles ?

Un exercice mathématique classique consiste à démontrer qu'on trouve les trois lois de Kepler pour un corps en mouvement à partir du moment où on admet que ce corps est soumis à une accélération inversement proportionnelle au carré de sa distance à un point fixe, et dirigée vers ce point. On parle d'accélération en 1/r² (prononcé « un sur r deux »). Pour un même corps placé dans différentes conditions initiales, la troisième loi s'applique, avec un coefficient dépendant du problème.

Cas de la gravitation

En admettant que le Soleil est infiniment lourd par rapport aux planètes, et en négligeant leurs interactions entre elles, on constate que les planètes sont soumises aux trois lois.

De plus, en combinant le principe fondamental de la dynamique (deuxième loi de Newton) et la loi universelle de la gravitation, on trouve que l'accélération est indépendante de la masse du corps mobile dans le cas d'un mouvement pour lequel la force qui s'applique est la gravité. En conséquence, la constante de la troisième loi est la même pour toutes les planètes.

On peut appliquer les lois de Kepler pour tout autre objet central ; seule la constante de la troisième loi change. C'est le cas, par exemple, de la Lune et de la Terre ou d'un satellite artificiel en orbite autour de celle-ci ou pour les multiples lunes de Saturne.

Problème à deux corps

Les lois de Kepler peuvent aussi s'appliquer dans le cas d'un problème à deux corps. Simplement, dans ce cas, le point central auxquelles se réfèrent les deux premières lois n'est pas le centre du corps le plus massif, mais le centre de masse des deux objets.

Cas de forces autres que la gravitation

Comme on l'a dit plus haut, les lois de Kepler ne sont pas limitées à la gravitation. Elles s'appliquent pour toute accélération en 1/r². Or c'est aussi le cas de la loi de Coulomb en électrostatique.

Les lois de Kepler s'appliquent donc aussi aux électrons orbitant autour d'un noyau atomique. Le modèle de Bohr–Sommerfeld prévoit d'ailleurs des orbites elliptiques pour les électrons.

Par contre, on n'a plus indépendance par rapport à la masse du corps mobile. La constante dans la troisième loi dépend des constantes de la force, et de la masse (indépendante d'un électron à l'autre).

Toutefois aujourd'hui, la physique quantique considère que les électrons en orbite elliptique autour du noyau n'est qu'une approximation autrefois utile.

Forme newtonienne de la troisième loi de Kepler

Isaac Newton comprit le lien entre les lois de la mécanique classique et la troisième loi de Kepler. Il en déduisit la formule suivante :

,

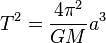
où

• T est la période de l'objet,
• a est le demi grand axe de la trajectoire elliptique,
• G est la constante de la gravitation universelle,
• M est la masse de l'objet au centre (en l'occurrence le Soleil si l'on applique la loi aux planètes)

Découverte de nouveaux corps célestes

Johannes Kepler découvrit ses lois grâce à un travail d'analyse considérable des tables astronomiques établies par Tycho Brahe. En particulier l'étude de Mars lui permit de montrer que le mouvement n'était pas épicyclique mais elliptique.

Ses lois ont permis, elles-mêmes, d'affiner les recherches astronomiques et de mettre en évidence des irrégularités de mouvements de corps connus, par une étonnante progression de l'analyse.

L'exemple le plus spectaculaire fut celui des irrégularités d'Uranus qui permit la « découverte » de Neptune par Le Verrier (1811 - 1877), par le calcul : découverte confirmée par l'observation de Galle (1812 - 1910) en 1846.