Loi uniforme continue - Définition

Distributions associées

Le théorème suivant stipule que toutes les distributions sont liées à la loi uniforme:

Pour une variable aléatoire de fonction de répartition F, on note G sa pseudo-inverse: . Si désigne une variable aléatoire réelle uniforme sur [0,1], alors a pour fonction de répartition .

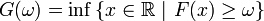
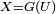
Bref, pour obtenir des tirages (indépendants) selon la loi caractérisée par F, il suffit d'inverser cette fonction et de l'appliquer à des tirages (indépendants) uniformes.

Voici quelques exemples de cette loi:

• Y = -ln(U)/λ est distribué selon la Loi exponentielle de paramètre λ;
• Y = 1 - U^1/n est distribué selon la Loi bêta de paramètres 1 et n. Ceci implique donc que la loi uniforme standard est un cas spécial de la loi bêta, de paramètres 1 et 1.