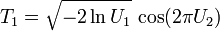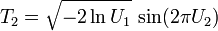Loi normale - Définition

Stabilité de la loi normale par la somme

La somme de deux variables gaussiennes indépendantes est elle-même une variable gaussienne. Plus explicitement :

Soient deux variables aléatoires indépendantes suivant respectivement les lois et .

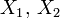
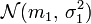
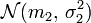
Alors, la variable aléatoire suit la loi normale .

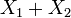
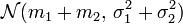
Cette propriété se démontre directement (par convolution), ou indirectement (au moyen des fonctions caractéristiques).

Exemple

On prend ici le gramme comme unité de masse. Si la masse du contenu d'une boîte de conserve suit la loi normale d'espérance 400 et de variance 25, et si celle du contenant suit la loi normale d'espérance 60 et de variance 4, alors (avec l'hypothèse, naturelle, d'indépendance) la masse totale de la boîte de conserve suit la loi normale d'espérance 460 et de variance 29 ; son écart type est environ 5,4 grammes.

Critères et tests de normalité

Critères de normalité

Le recours à une distribution gaussienne est si fréquent qu'il peut finir par être abusif. Il faut alors rechercher des critères de normalité.

Le premier critère, le plus simple, consiste à tracer l'histogramme ou le diagramme en bâtons de la distribution et à vérifier si le diagramme est en forme de « cloche ». Ce critère, subjectif, permet cependant d'éliminer une partie des distributions jugées alors non gaussiennes.

Le critère suivant consiste à utiliser les plages de normalité ou intervalles de confiance. On a vu que si une distribution est gaussienne :

• 68% de la population est dans l'intervalle ,

• 76% de la population est dans l'intervalle ,

• 95% de la population est dans l'intervalle ,

• 99% de la population est dans l'intervalle .

Lorsque ces pourcentages ne sont pas respectés, il y a fort à parier que la distribution n'est pas gaussienne.

On peut aussi utiliser la droite de Henry, en particulier quand on possède peu de renseignements sur la distribution. La droite de Henry va permettre de porter un diagnostic sur la nature non gaussienne de la distribution, et, dans le cas où celle-ci a des chances d'être gaussienne, elle permet d'en déterminer la moyenne et l'écart type.

Tests de normalité

Il existe également un grand nombre de tests de normalité:

• Tests basés sur la fonction de répartition empirique : Test de Kolmogorov-Smirnov et son adaptation le test de Lilliefors (en), ou le test de Anderson-Darling (en)

• Tests basés sur les moments, comme le Test de Jarque Bera ou test D'Agostino's K-squared (en)

• Test d'adéquation du χ²

• ou encore le test de Shapiro-Wilk (en)

Stabilité de la loi normale par la moyenne

Soient des variables aléatoires indépendantes suivant respectivement les lois normales

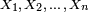
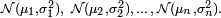
La moyenne suit alors la loi

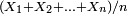
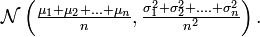
Simulation

Il est possible de simuler, par exemple par ordinateur, un tirage aléatoire dont la loi est normale.

Les logiciels ou les langages de programmation possèdent en général un générateur de nombres pseudo-aléatoires ayant une distribution uniforme sur ]0,1[. On cherche donc une fonction transformant ces nombres. De manière générale, on peut prendre la fonction réciproque de la fonction de répartition : en l'occurrence, si la variable aléatoire U suit la loi uniforme sur ]0,1[, alors la variable aléatoire suit la loi normale centrée réduite ; cependant, cette méthode est tout à fait malcommode, faute d'expressions simples des fonctions et . En revanche, on peut facilement utiliser la méthode décrite ci-dessous.

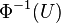
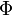
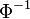
Cas de la loi normale à une dimension

Pour simuler la loi normale à une dimension (celle qui a été étudiée jusqu'ici), on peut utiliser la méthode de Box-Muller dont voici le principe :
Si U₁ et U₂ sont des variables aléatoires indépendantes qui suivent la loi uniforme sur ]0,1[, alors on démontre assez aisément que les variables aléatoires :

suivent toutes deux la loi normale centrée réduite (et sont indépendantes).

Les variables aléatoires et suivent donc toutes deux la loi normale , et indépendamment l'une de l'autre.

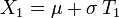
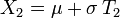
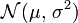
Exemple d'implémentation

      #define DEUX_PI ( 2.0 * 3.141592653589793238462643383279502884197169399375 ) // PI x 2             // [ ... ]             /**       * Retourne un nombre pseudo-aléatoire selon une loi normale de paramètres mu et sigma       * @param mu moyenne (espérance mathématique) de la distribution       * @param sigma écart-type de la distribution (doit être strictement positif)       */      double genererNombreLoiNormale(double mu, double sigma) {             	// On récupère deux nombres pseudo-aléatoires indépendants selon une loi uniforme sur l'intervalle [0;1]      	double randNumUni = ((double) rand())/((double) RAND_MAX);      	double randNumBi = ((double) rand())/((double) RAND_MAX);             	// On récupère un nombre pseudo-aléatoire selon une loi normale centrée réduite      	// (Paramètres: moyenne = 0, écart-type = 1)      	// Utilisation de l'algorithme de Box-Muller      	double randNumNorm = sqrt(-2.0*log(randNumUni))*cos(DEUX_PI*randNumBi);             	return (mu + sigma * randNumNorm);      }      

Voir aussi

• (fr) Générateur de nombres aléatoires gaussiens, message de news:fr.sci.maths, 27 janvier 2000 ;
• (en) Generating Gaussian Random Numbers

Cas de la loi multinormale

La loi multinormale ou loi normale sur étend la loi normale à un vecteur aléatoire à valeurs dans .

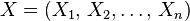
Elle est caractérisée par deux paramètres : un vecteur m de moyennes, et une matrice de variance-covariance V (carrée d'ordre n).

Pour simuler une loi multinormale non dégénérée de paramètres m et V, on utilise la méthode suivante :

1. Soit T un vecteur aléatoire à n composantes gaussiennes centrées réduites et indépendantes (la loi de T, multinormale, a pour moyenne le vecteur nul et pour matrice de variance-covariance la matrice identité).
2. Soit L la matrice résultant de la factorisation de Cholesky de la matrice V.
3. Alors, le vecteur aléatoire X = m + LT suit la loi multinormale de moyenne m et de variance-covariance V

(on convient dans cette dernière relation d'identifier chaque élément de avec la matrice colonne de ses composantes en base canonique).