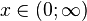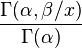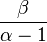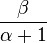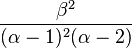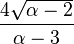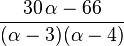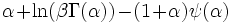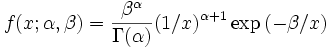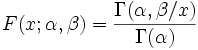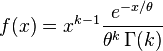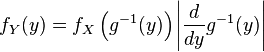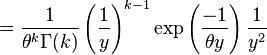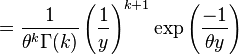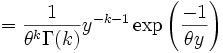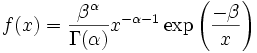Loi inverse-gamma - Définition

Introduction

Inverse-gamma
Paramètres	α > 0 paramètre de forme (réel) β > 0 paramètre d'échelle (réel)
Support
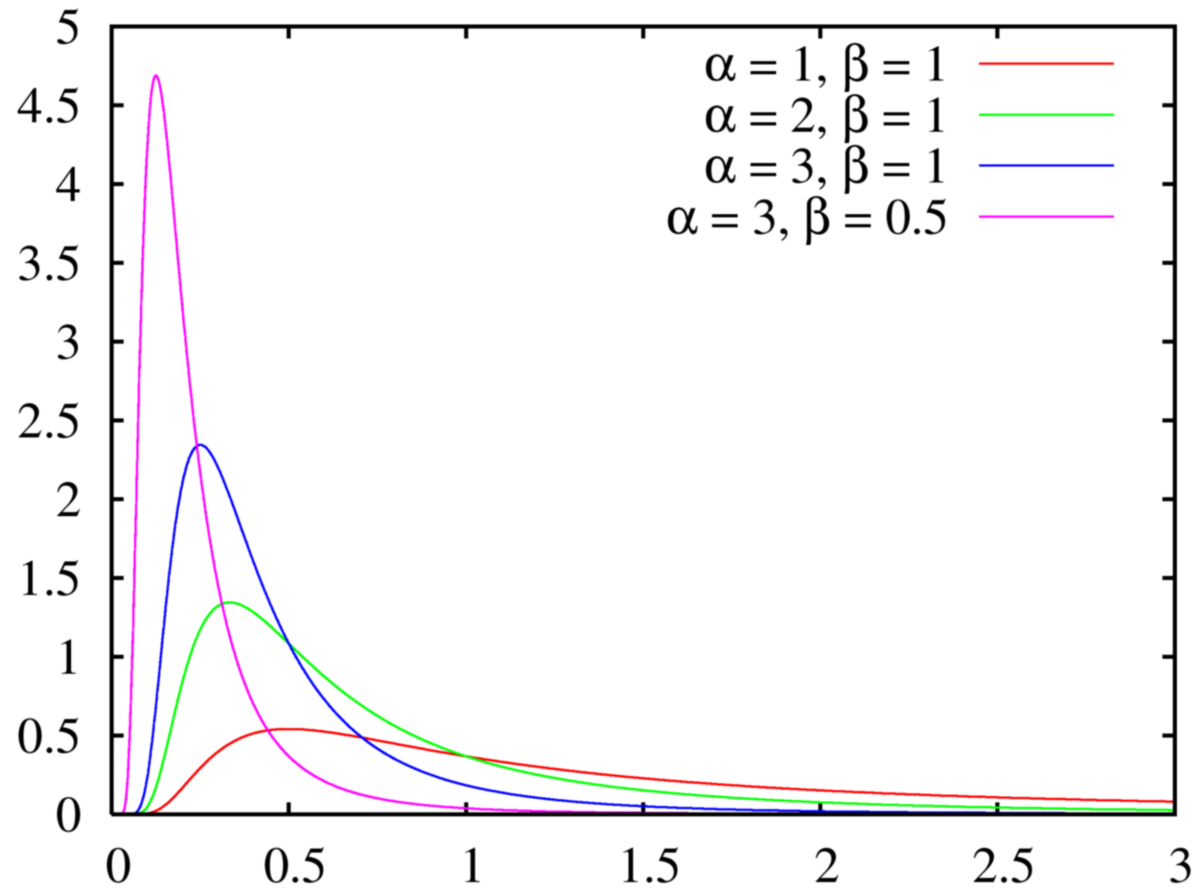
Densité de probabilité (fonction de masse)
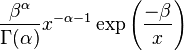
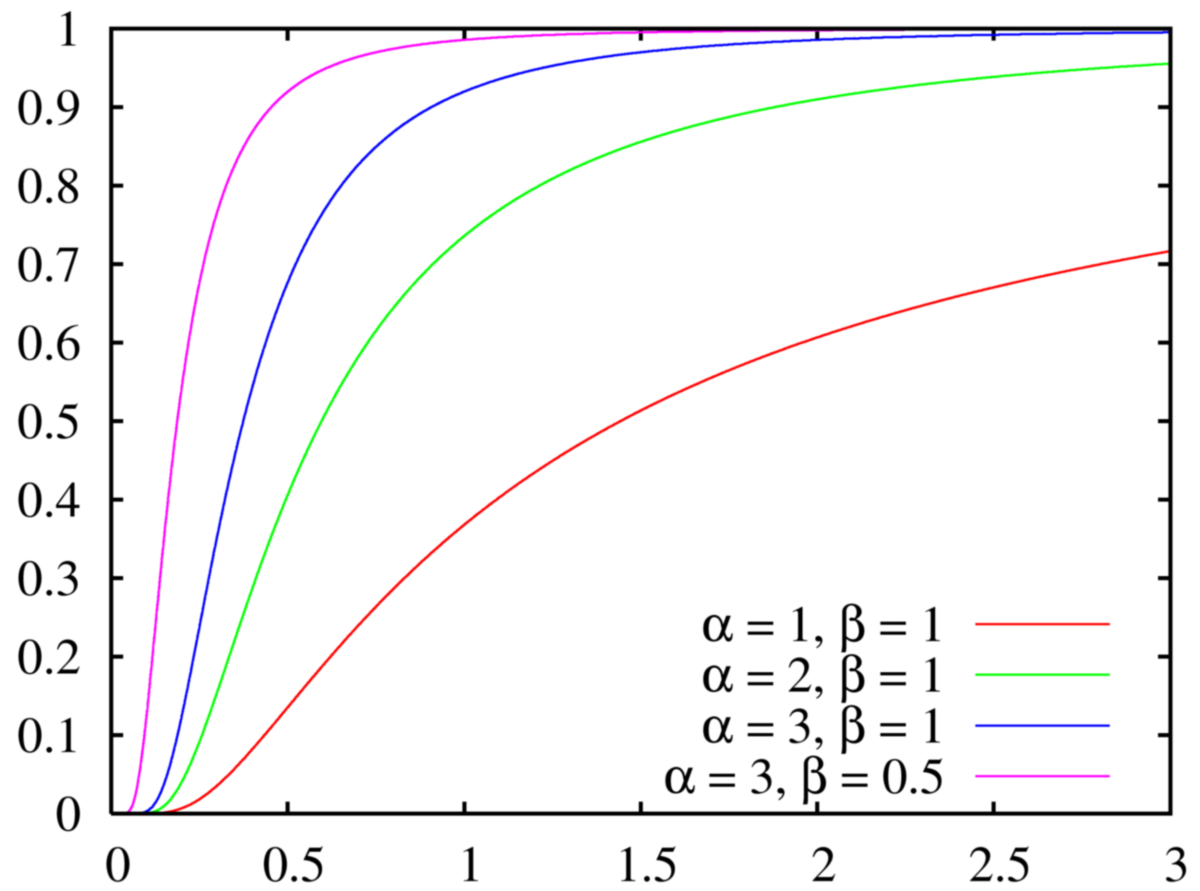
Fonction de répartition
Espérance	pour α > 1
Mode
Variance	pour α > 2
Asymétrie (statistique)	pour α > 3
Kurtosis (non-normalisé)	pour α > 4
Entropie
Fonction génératrice des moments
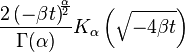
Fonction caractéristique
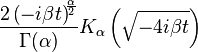
modifier

Dans la Théorie des probabilités et en Statistiques, la distribution inverse-gamma est une famille de lois de probabilité continues à deux paramètres sur la demi-droite des réels positifs. Il s'agit de l'inverse d'une variable aléatoire distribuée selon une Distribution Gamma.

Caractérisation

Densité de probabilité

La Densité de probabilité de la loi inverse-gamma est définie sur le support x > 0 par:

où α est un Paramètre de forme et β un paramètre d'intensité, c'est-à-dire l'inverse d'un Paramètre d'échelle.

Fonction de répartition

La Fonction de répartition est la Fonction gamma régularisée:

où le numérateur est la fonction gamma incomplète et le dénominateur est la Fonction gamma.

Obtention à partir de la loi Gamma

La densité de la loi gamma est

et définissons la transformation . La densité de la transformée est alors

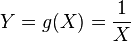
Remplaçant k par α, θ ^{− 1} par β et enfin y par x donne la densité donnée plus haut:

Distributions associées

• Si X˜Inv-Gamma(α,β) et alors est une loi du chi-deux (χ²) inverse;
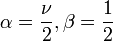
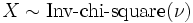
• Si , alors ;
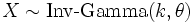
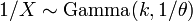
• Une généralisation multivariée de la loi inverse-gamma est la distribution Wishart inverse;