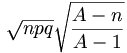Loi hypergéométrique - Définition
La liste des auteurs de cet article est disponible ici.
Espérance, variance et écart type
L'espérance d'une variable aléatoire suivant une loi hypergéométrique est la même que dans le cas binômiale.

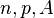
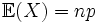
On se donne:
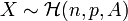
(si on se rapporte à un modèle d'urnes à tirage simultané, c'est-à-dire non ordonné et sans remise. On a donc
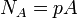
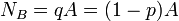
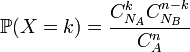
Numérotons de 1 à
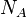
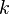
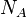
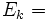

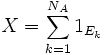
(où 1 est la Fonction indicatrice de
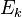
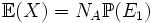
Évaluons maintenant
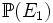
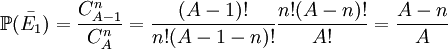
Donc
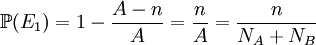
On en conclut donc que
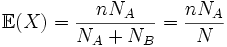
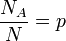
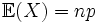
La variance d'une variable aléatoire suivant une loi hypergéométrique de paramètres n, p, A est
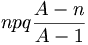
L'écart type est alors