Loi forte des grands nombres - Définition
La liste des auteurs de cet article est disponible ici.
Démonstration de la loi forte de Kolmogorov
1ère étape de la démonstration : troncature
On suppose tout d'abord que les variables
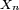
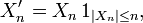
et
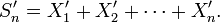
Dans cette section on démontre que
Proposition 1. — Soit une suite
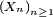
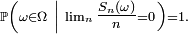
- est équivalente à
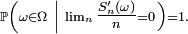
Posons
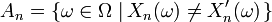
Alors
![\begin{align} \sum_{n\ge1}\,\mathbb{P}\left(A_{n}\right) &= \sum_{n\ge1}\,\mathbb{P}\left(X_{n}\neq X^{\prime}_{n}\right) \\ &= \sum_{n\ge1}\,\mathbb{P}\left(\left|X_{n}\right|>n\right) \\ &= \sum_{n\ge1}\,\mathbb{P}\left(\left|X_{1}\right|>n\right) \\ &= \sum_{n\ge1}\,\mathbb{E}\left[1_{\left|X_{1}\right|>n}\right] \\ &= \mathbb{E}\left[\sum_{n\ge1}\,1_{\left|X_{1}\right|>n}\right], \end{align}](https://upload.wikimedia.org/math/d/f/9/df999a7cba14b4109809bf8c5eb9761a.png)
la 3ème égalité car
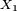
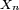
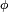
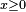

satisfait, pour
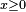
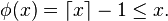
Ainsi
![\begin{align} \sum_{n\ge1}\,\mathbb{P}\left(A_{n}\right) &= \mathbb{E}\left[\sum_{n\ge1}\,1_{\left|X_{1}\right|>n}\right] \\ &= \mathbb{E}\left[\phi\left(\left|X_{1}\right|\right)\right] \\ &\le \mathbb{E}\left[\left|X_{1}\right|\right]<+\infty. \end{align}](https://upload.wikimedia.org/math/0/1/b/01b99d00ef0cf491e0a5d2a2b18455ef.png)
En vertu du lemme de Borel-Cantelli, il suit que
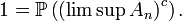
On note
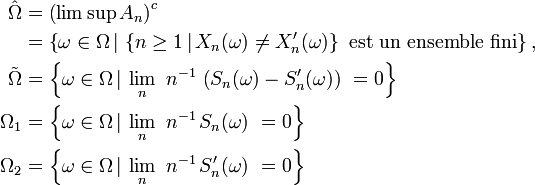
et on remarque que si
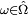
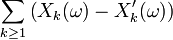
est une série convergente, puisque, en dehors d'un nombre fini d'entre eux, tous ses termes sont nuls. Ainsi la suite des sommes partielles,
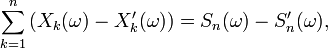
est une suite convergente, donc bornée, ce qui entraîne que
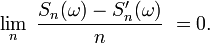
Autrement dit, en vertu de la première partie de cette démonstration,
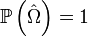
Les quelques lignes qui précèdent montrent que
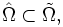
il suit donc que
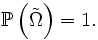
Par ailleurs, il est clair que
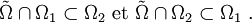
On a donc bien
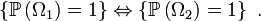
Dans les sections suivantes on va donc démontrer que
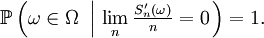
L'idée est que plus les variables concernées sont intégrables, i.e. plus la queue de distribution
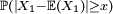
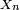
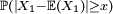

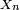
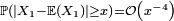
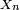
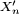
2ème étape de la démonstration : recentrage
Les
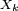
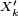
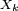
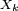
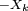
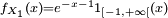
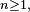
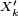
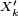
![Z_{k}= X^{\prime}_{k}-\mathbb{E}\left[X^{\prime}_{k}\right],](https://static.techno-science.net/illustration/Definitions/autres/6/6da0eb2fcc2e47186c6eb9c2d73995b5_eae26bc0023e25527fcb20a5cfb31d01.png)
et
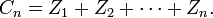
Alors
Proposition 2. — Soit une suite
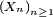
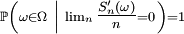
- est équivalent à
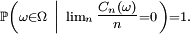
Un calcul simple donne que
![\begin{align} \frac{S^{\prime}_{n}(\omega)}n-\frac{C_{n}(\omega)}n &= \frac{\mathbb{E}\left[X^{\prime}_{1}\right]+\mathbb{E}\left[X^{\prime}_{2}\right]+\dots+\mathbb{E}\left[X^{\prime}_{n}\right]}n, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/502816f86c3674f26453985120ca1a65_e861bbbc21926ca10a8bd081180bbc9b.png)
la différence ne dépendant pas de

![\lim_{n}\mathbb{E}\left[X^{\prime}_{n}\right]=\lim_{n}\mathbb{E}\left[X_{n}1_{\left|X_{n}\right|\le n}\right]=\lim_{n}\mathbb{E}\left[X_{1}1_{\left|X_{1}\right|\le n}\right]=0.](https://static.techno-science.net/illustration/Definitions/autres/4/4e5ec7391380b46a48a08fd078cc35a0_d3bdf714b2798790a9122f8d36c14fed.png)
En effet
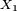
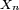
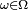
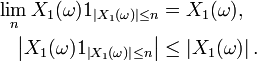
On peut donc appliquer le Théorème de convergence dominée de Lebesgue, et obtenir
![\lim_{n}\mathbb{E}\left[X^{\prime}_{n}\right]=\lim_{n}\mathbb{E}\left[X_{1}1_{\left|X_{1}\right|\le n}\right]=\mathbb{E}\left[\lim_{n}\,X_{1}1_{\left|X_{1}\right|\le n}\right]=\mathbb{E}\left[X_{1}\right]=0.](https://static.techno-science.net/illustration/Definitions/autres/d/dc1ccbc7042076ad9db649663943ccd1_14d1f42a5df36f364f78d9abd3889781.png)
Finalement, on sait, en vertu du lemme de Cesàro, que la convergence d'une suite (
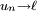
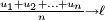
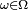
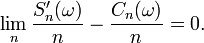
La Proposition 2 est donc démontrée.
3ème étape : Inégalité de Kolmogorov
C'est l'étape où Kolmogorov utilise l'hypothèse d'indépendance (et, sans le dire, la notion de temps d'arrêt). Par contre, l'Inégalité de Kolmogorov ne requiert pas des variables de même loi.
Inégalité de Kolmogorov. — Soit une suite
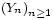
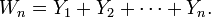
Alors, pour tout  ,
,

Si
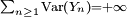
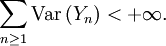
On pose

On remarque alors que, pour
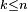
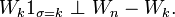
En effet
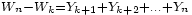

Ainsi pour deux boréliens quelconques
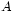
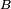
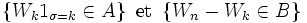
appartiennent aux tribus
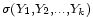
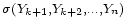
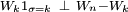
![\begin{align} \sum_{k=1}^n\,\text{Var}\left(Y_{k}\right) &= \text{Var}\left(W_{n}\right)\ =\ \mathbb{E}\left[W_{n}^2\right] \\ &\ge \mathbb{E}\left[W_{n}^21_{\sigma<+\infty}\right] \\ &= \sum_{k\ge1}\ \mathbb{E}\left[W_{n}^2\ 1_{\sigma=k}\right] \\ &\ge \sum_{k=1}^n\ \mathbb{E}\left[W_{n}^21_{\sigma=k}\right] \\ &= \sum_{k=1}^n\ \mathbb{E}\left[\left(W_{n}-W_{k}+W_{k}\right)^21_{\sigma=k}\right] \\ &\ge \sum_{k=1}^n\ \mathbb{E}\left[W_{k}^21_{\sigma=k}\right]+2\mathbb{E}\left[W_{n}-W_{k}\right]\mathbb{E}\left[W_{k}1_{\sigma=k}\right] \\ &= \sum_{k=1}^n\ \mathbb{E}\left[W_{k}^21_{\sigma=k}\right] \\ &\ge \sum_{k=1}^n\ \mathbb{E}\left[x^21_{\sigma=k}\right] \\ &= x^2\mathbb{P}\left(\sigma\le n\right), \end{align}](https://static.techno-science.net/illustration/Definitions/autres/6/69997ff92ae4f3d4eea979688e1b482c_859f1faeaa76d080f815ed3c6f857463.png)
où la troisième inégalité s'obtient en développant le carré en deux termes carrés (dont l'un est supprimé pour minorer l'expression précédente) et un double produit (de deux variables indépendantes, en vertu de
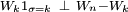
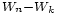


 . En faisant tendre
. En faisant tendre

C.Q.F.D.
Voir aussi l'article en anglais sur le même sujet.
4ème étape : Convergence de séries de variables aléatoires
L'inégalité de Kolmogorov est, avec le lemme de Borel-Cantelli, l'ingrédient essentiel de la preuve de la proposition suivante :
Proposition 3. — Soit une suite
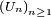
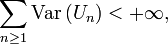
alors la suite
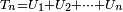
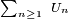
On pose
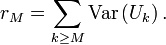
En vertu de la convergence de la série de terme général
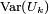
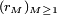
Avec les notations de l'inégalité de Kolmogorov, on a
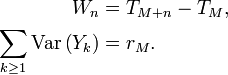
Donc l'inégalité de Kolmogorov nous donne, pour tout  et
et
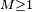

Notons que la suite de variables aléatoires
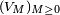

est décroissante, puisque la suite d'ensembles
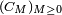

est décroissante. De plus
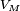
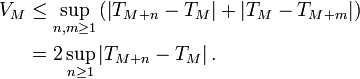
On en déduit que, pour tout
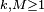

La suite
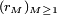
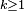
 tel que
tel que

Ainsi

et le lemme de Borel-Cantelli entraîne que, presque sûrement, à partir d'un certain rang,
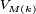
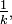
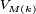

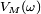
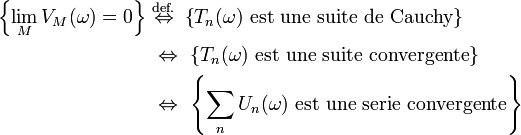
C.Q.F.D.
5ème étape : Lemme de Kronecker
Lemme de Kronecker. — Soit une suite
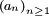
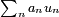
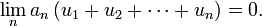
La démonstration ci-dessous vaut seulement pour
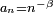
 , mais la démonstration de la loi forte utilise le lemme de Kronecker pour
, mais la démonstration de la loi forte utilise le lemme de Kronecker pour
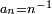
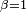
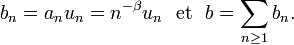
Alors
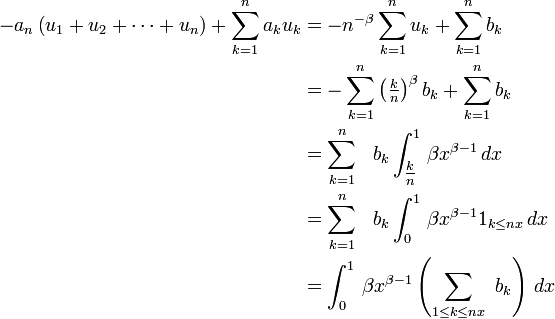
Comme la suite
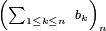
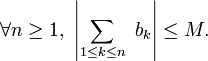
Donc la suite de fonctions
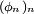
![\ \scriptstyle [0,1] \](https://static.techno-science.net/illustration/Definitions/autres/9/911312ad6fe325a8c9894661a9f2502e_b90b16babfb5cd9480d16024e355fa18.png)
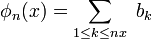
est une suite de fonctions uniformément bornées par
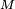
![\ \scriptstyle x\in[0,1] \](https://static.techno-science.net/illustration/Definitions/autres/d/d731b25851e592b89875d870e80d17b7_faac3b9dd741e4a532842f6f04786b3d.png)

Ainsi le théorème de convergence dominée de Lebesgue donne

Comme on a
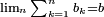
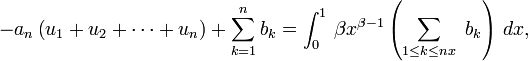
démontrée plus haut, on en déduit que
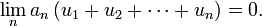
C.Q.F.D.
Cette démonstration est empruntée à Sydney Resnik, A probability path.
Pour conclure sa démonstration, Kolmogorov utilise le lemme de Kronecker avec
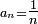
6ème étape : Conclusion dans le cas de variables centrées
Lemme 1. — Avec les notations de l'étape "recentrage", on a
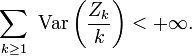
Les calculs s'arrangent mieux si on remplace

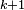
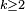
![\text{Var}\left(\frac{Z_{k}}{k+1}\right)\ = \ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2}\ - \ \frac{\mathbb{E}\left[X^{\prime}_{k}\right]^2}{(k+1)^2}.](https://static.techno-science.net/illustration/Definitions/autres/8/82e0076fc76bf5079ac035172a90f2e1_616397a62156409e8148dc0ade4b394f.png)
Comme
![\ \scriptstyle \lim_{n} \mathbb{E}\left[X^{\prime}_{n}\right]=0 \](https://static.techno-science.net/illustration/Definitions/autres/7/78b8802a904b56a14d1b8c828be8e2ec_2ff0056ca2c5c276dcecc23279664ce6.png)
![\frac{\mathbb{E}\left[X^{\prime}_{k}\right]^2}{(k+1)^2}=o\left(\frac{1}{k^2}\right),](https://static.techno-science.net/illustration/Definitions/autres/4/4100b798acdbc4cd2b9a4c5f2a060e77_f06faf49755a4f5e37dcbe82e68aebe0.png)
et la convergence de la série
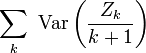
est équivalente à la convergence de la série
![\sum_{k}\ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2}.](https://static.techno-science.net/illustration/Definitions/autres/5/59a3d7d6bcf2debe709a405a713f8b17_a95f410f1163d52194c5d88985bbd595.png)
Or
![\begin{align} \sum_{k\ge 1}\ \frac{\mathbb{E}\left[X^{\prime 2}_{k}\right]}{(k+1)^2} &= \sum_{k\ge 1}\ (k+1)^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le k}\right] \\ &\le \sum_{k\ge 1}\ \int_{k}^{k+1}x^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le x}\right]\ dx \\ &= \int_{1}^{+\infty}x^{-2}\ \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|\le x}\right]\ dx \\ &= \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\ \int_{1}^{+\infty}x^{-2}\ 1_{\left|X_{1}\right|\le x}\ dx\right] \\ &\le \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\ \int_{\left|X_{1}\right|}^{+\infty}\ x^{-2}\ dx\right] \\ &= \mathbb{E}\left[X^{2}_{1}\,1_{0<\left|X_{1}\right|}\left|X_{1}\right|^{-1}\right] \\ &= \mathbb{E}\left[\left|X_{1}\right|\right]\ <\ +\infty, \end{align}](https://static.techno-science.net/illustration/Definitions/autres/5/51a4ba1b40c461db1563175e906fd06d_9202a5ff080e6a47ebf31f89d5472eb5.png)
par hypothèse.
Du Lemme 1 et de la Proposition 3, on déduit que, presque sûrement,
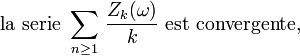
puis, grâce au lemme de Kronecker, on déduit que, presque sûrement,
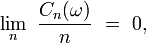
ce qui est équivalent à la loi forte des grands nombres (pour des variables centrées), comme on l'a vu aux étapes "troncature" et "recentrage".
7ème étape : décentrage
Si on ne suppose plus les
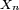
![\hat{X}_{k}= X_{k}-\mathbb{E}\left[X_{k}\right],\ \ \hat{S}_{n}= \hat{X}_{1}+\hat{X}_{2}+\cdots+\hat{X}_{n},](https://static.techno-science.net/illustration/Definitions/autres/0/0a70ae910d3dde1d6c6a09bfd2d82817_ca04fdfc6ffd594fb0367a86b2842090.png)
et, les étant centrées, i.i.d. et intégrables, la conclusion des étapes précédentes est que
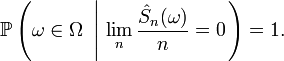
Mais
![\begin{align} \frac{\hat{S}_{n}(\omega)}n &= \frac{S_{n}(\omega)-n\mathbb{E}\left[X_{1}\right]}n \\ &= \frac{S_{n}(\omega)}n\ -\ \mathbb{E}\left[X_{1}\right]. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/f/fe60cbc818cb8ade19cbae7c09762e1d_5b53e23af7c8703b69baf6ded2c0a691.png)
Donc
![\mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\frac{\hat{S}_{n}(\omega)}n=0\right.\right) = \mathbb{P}\left(\omega\in\Omega\ \left|\ \lim_{n}\frac{S_{n}(\omega)}n=\mathbb{E}\left[X_{1}\right]\right.\right) .](https://static.techno-science.net/illustration/Definitions/autres/7/790887b5427aee7f65a72c5365beaba3_77e5c5f5f656732c48b8488314c04476.png)
C.Q.F.D.
Réciproque
Supposons que l'ensemble Ωc défini par
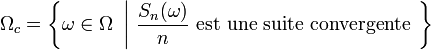
est de probabilité 1. Notons l(ω) la limite de la suite ci-dessus, lorsqu'elle est définie, i.e. lorsqu' ω appartient à Ωc . L'ensemble Ωc est inclus dans l'ensemble suivant
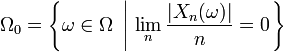
puisque, lorsqu' ω appartient à Ωc , on a
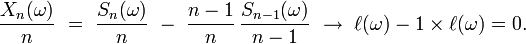
Ainsi, l'ensemble Ω0 lui aussi est de probabilité 1. Posons

La limite supérieure des An est disjointe de l'ensemble Ω0 , donc elle est de probabilité nulle. En vertu de la loi du zéro-un de Borel, on en déduit, puisque les événements An sont indépendants, que

Par ailleurs, en toute généralité, comme on l'a vu lors de la ,
![\sum_{n\ge 1}\mathbb{P}\left(|X_{n}|>n\right)\ =\ \sum_{n\ge 1}\mathbb{P}\left(|X_{1}|>n\right)\ =\ \mathbb{E}\left[\left\lceil|X_{1}|\right\rceil-1\right]\ \ge\ -1+\mathbb{E}\left[|X_{1}|\right].](https://upload.wikimedia.org/math/e/6/1/e61ea338826b807c476258384b2a2d1c.png)