Loi exponentielle - Définition
La liste des auteurs de cet article est disponible ici.
Lien avec la loi géométrique
La loi géométrique est une version discrétisée de la loi exponentielle. En conséquence, la loi exponentielle est une limite de lois géométriques renormalisées.
Propriété — Si

 alors
alors
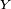
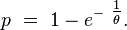
![\begin{align} \mathbb{P}(Y=k) &= \mathbb{P}(\lceil\theta X\rceil=k) \\ &= \mathbb{P}(\theta X\in]k-1,k]) \\ &= \mathbb{P}\left(X\in\left]\tfrac{k-1}{\theta},\tfrac{k}{\theta}\right]\right) \\ &= F_X\left(\tfrac{k}{\theta}\right)-F_X\left(\tfrac{k-1}{\theta}\right) \\ &= \exp\left(-\ \tfrac{k-1}{\theta}\right)-\exp\left(-\ \tfrac{k}{\theta}\right) \\ &= \left(e^{-\ \tfrac{1}{\theta}}\right)^{k-1}\ \left(1-e^{-\ \tfrac{1}{\theta}}\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/9/9ac8df3782b0bc151637ec756d95e6e0_6751db92dc86507dd2cce6bff879294b.png)
Notons que, pour un nombre réel
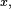
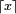
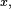
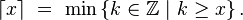
En choisissant
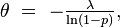
on fabrique ainsi, à partir d'une variable aléatoire exponentielle
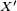
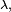
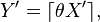
suivant une loi géométrique de paramètre

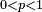
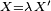
Réciproquement,
Propriété — Si, pour
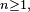
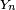
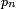

alors
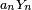
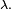
On se donne une variable aléatoire exponentielle

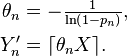
Alors
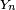
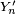
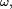
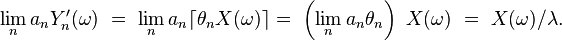
Or d'une part la convergence presque sûre entraine la convergence en loi, d'autre part la loi de
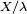
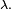
On peut voir ces différentes convergences comme de simples conséquences de la convergence du schéma de Bernoulli vers le processus de Poisson.
Durée de vie minimale
Si les variables aléatoires X, Y sont indépendantes et suivent deux lois exponentielles de paramètres λ, μ, alors Z = inf(X; Y) est une variable aléatoire qui suit la loi exponentielle de paramètre λ + μ.
Cette observation est très utile pour déterminer l'espérance de vie d'un système constitué de deux composants en série.

















































