Loi des grands nombres - Définition
La liste des auteurs de cet article est disponible ici.
Loi forte des grands nombres
Considérons une suite
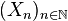
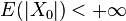
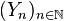
C’est-à-dire que :
Théorème —
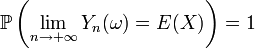
Autrement dit, selon la loi forte des grands nombres, la moyenne empirique est un estimateur fortement convergent de l'espérance.
Loi faible des grands nombres
La loi faible des grands nombres est également appelée théorème de Khintchine (rarement utilisé).
On considère une suite
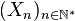
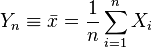
Théorème — 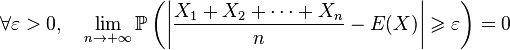
Autrement dit,
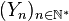
La loi faible des grands nombres se démontre en utilisant l'inégalité de Bienaymé-Tchebychev :
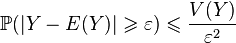
On remarque que la variable aléatoire
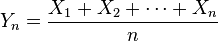
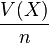
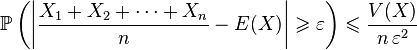
Convergence vers une loi de probabilité
La loi des grands nombres permet de dire que la répartition de la population de l'échantillon peut être approchée par la loi de probabilité de X pour n assez grand.
En effet, pour tout i, la fréquence fn(i) de la valeur xi dans l'échantillon
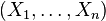
Pour le prouver, on fixe désormais i et l'on considère pour tout k la variable aléatoire Bk indicatrice de l'évènement (Xk = xi).
Cela signifie (par définition) que Bk(ω) = 1 si Xk(ω) = xi et Bk(ω) = 0 si
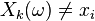
La suite (Bk) est constituée de variables aléatoires indépendantes suivant la même loi de Bernoulli de paramètre pi ; elles possèdent une variance finie et leur espérance commune est E(B) = pi.
Or, pour tout n,
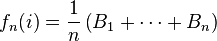
- en probabilité (d'après la loi faible des grands nombres)
- presque sûrement (d'après la loi forte des grands nombres)

















































