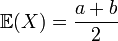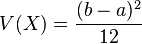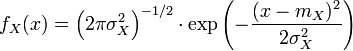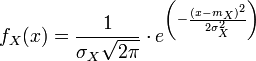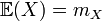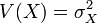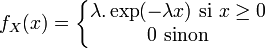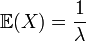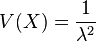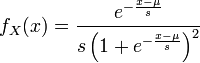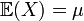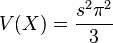Loi de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des probabilités et en statistique, une loi de probabilité décrit soit les probabilités de chaque valeur d'une variable aléatoire (quand la variable aléatoire est discrète), soit la probabilité que la variable aléatoire appartienne à un intervalle arbitraire (quand la variable est continue). La loi de probabilité décrit l'ensemble des valeurs qu'une variable aléatoire peut atteindre et la probabilité que la valeur de la variable aléatoire soit dans n'importe quel sous ensemble (mesurable) de cet ensemble.
Quand la variable aléatoire prend ses valeurs dans
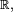
Le concept de loi de probabilité (et le concept de variable aléatoire) sont les fondements des disciplines mathématiques appelées théorie des probabilités, et statistique. Il y a de la fluctuation ou de la variabilité dans presque toute valeur qui peut être mesurée dans une population (par exemple la taille des individus, la durabilité d'une pièce de métal, etc.) ; presque toutes les mesures ont une part d'erreur intrinsèque ; en physique, de nombreux processus ont une description probabiliste, de la théorie cinétique des gaz à la description quantique des particules élémentaires. Pour ces raisons en particulier, et pour beaucoup d'autres raisons, de simples nombres sont souvent inadéquats pour décrire une quantité, alors qu'une loi de probabilité est plus appropriée.
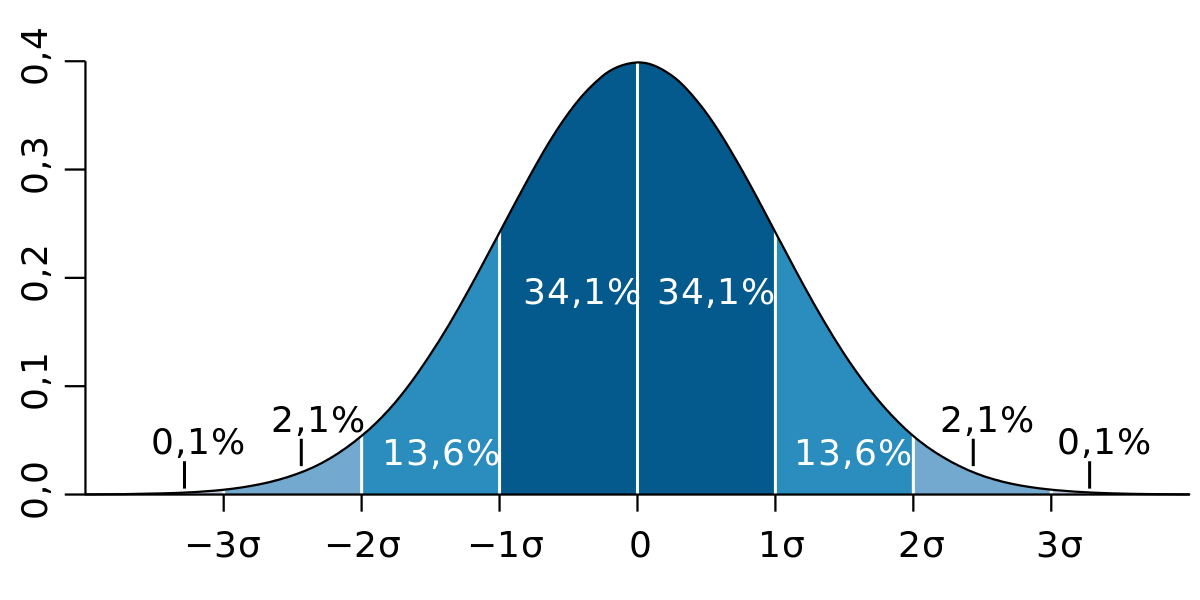
Bien des lois de probabilités apparaissent dans les applications. Une des plus importantes est la loi normale, qui est aussi connue sous le nom de distribution gaussienne ou de courbe en cloche et qui approxime de nombreuses lois de probabilités apparaissant dans les applications. Le jet d'une pièce donne lieu à une autre loi de probabilité naturelle, dont les valeurs possibles sont pile ou face, chacune avec probabilité 1/2.
Définition informelle
Une loi de probabilité se caractérise de différentes manières. Le plus souvent, on utilise la fonction de répartition pour caractériser une loi. Cela présente l'avantage d'être valable aussi bien pour les lois discrètes que continues. Dans le cas d'une loi continue, on utilise très souvent la densité, alors que dans le cas discret, la donnée des probabilités élémentaires suffit à caractériser la loi en question.
Exemples de lois à densité
Une variable aléatoire réelle

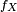
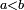
On dit aussi alors que la loi
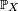

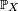
En conséquence,
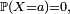
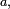
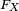

Les variables aléatoires à densité sont parfois appelées variables continues.
Loi uniforme
Loi uniforme continue sur un intervalle borné [a; b] :
Loi normale
Loi exponentielle
Loi logistique
Loi de Cauchy
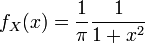
La loi de Cauchy n'admet aucun moment (donc ni moyenne ni variance, entre autres).
Loi de Tukey-Lambda
La Loi de Tukey-Lambda est connue de façon implicite par la distribution de ses quantiles :
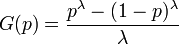
elle a par la suite été généralisée.
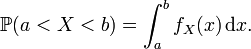
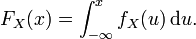
![f_X (x) = \left\{\begin{matrix} \frac{1}{b-a}& \mathrm{si}\ x \in [a;b] \\ 0& \mathrm{sinon} \end{matrix}\right.](https://static.techno-science.net/illustration/Definitions/autres/6/66a0d2505018eaef9eec431be7216c17_1a9395baf1a18d220dbec596ae637df3.png)