Loi de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Définition mathématique
En théorie des probabilités, une loi (ou mesure) de probabilité est une mesure positive

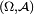
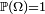
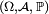
Définition — Soit une variable aléatoire réelle sur l'espace probabilisé
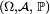
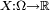
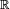
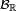

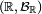
pour tout borélien
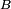
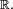


Deux variables aléatoires réelles

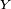
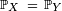
ou bien encore
Plus généralement, deux variables aléatoires réelles

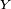
pour toute fonction
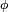
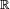
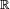
Théorème de transfert — Soit une variable aléatoire réelle
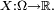
pour toute fonction
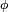
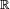
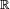
L'intégrale apparaissant dans le deuxième terme est l'intégrale, au sens de la théorie de la mesure, de la fonction φ par rapport à la mesure
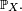
Histoire
L'allure générale des lois de probabilité usuelles fut au début observée empiriquement, puis on en formalisa la définition dans le cadre de la théorie des probabilités en mathématiques.
Classification des lois de probabilité sur la droite réelle
Les lois énumérées dans cet article sont des mesures de probabilités sur
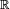
- lorsque la loi de la variable aléatoire X est portée par un ensemble S
-
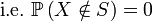
- tel que S est fini ou dénombrable, on parle de loi de probabilité discrète.
- D'un point de vue pratique, les calculs de probabilités ou bien d'espérances liées à

-
![\mathbb{P}\left(X\in A\right)=\sum_{x\in A\cap S}\ \mathbb{P}\left(X=x\right),\qquad\mathbb{E}\left[\phi(X)\right]=\sum_{x\in S}\ \phi(x)\mathbb{P}\left(X=x\right).](https://static.techno-science.net/illustration/Definitions/autres/3/3383874afdfabb7a44549f5c24c87a9b_1ec99073c6c35959e8932cbdb0974015.png)
- Pour une variable discrète, on peut choisir comme ensemble


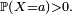
- La deuxième égalité ci-dessus est la spécialisation du au cas particulier des variables discrètes, puisque dans ce cas particulier, on a
-
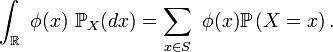
- lorsque la loi de




-
![\mathbb{P}\left(X\in A\right)=\int_{A}\ f_X(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=\int_{\mathbb{R}}\ \phi(x)\ f_X(x)\,dx.](https://static.techno-science.net/illustration/Definitions/autres/8/8afc23451ff6cf9d74e0fa62a2867023_ce835adc2b37457972f78a3a9b812ede.png)
- Là encore, la deuxième égalité ci-dessus est la spécialisation du , mais cette fois, au cas particulier des variables à densité, puisque dans ce cas particulier, on a
-
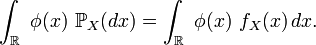
- Une variable à densité

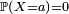
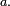
Il existe d'autres types de variables aléatoires réelles :
- la loi d'une variable aléatoire

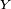

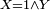

- dans le cas précédent, la fonction de répartition de la durée d'utilisation



 On voit que les variables à densité ont des fonctions de répartitions localement absolument continues, donc, a fortiori, continues sur
On voit que les variables à densité ont des fonctions de répartitions localement absolument continues, donc, a fortiori, continues sur
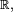
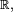
-
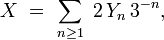
- où les
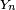


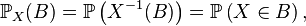
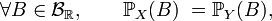
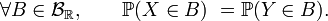
![\mathbb{E}\left[\phi(X)\right]\ = \mathbb{E}\left[\phi(Y)\right]](https://static.techno-science.net/illustration/Definitions/autres/4/422abfdc7c17520b9b63c57ef6319072_73dd15cb7aee06cdb47792afb6b89a64.png)
![\mathbb{E}\left[\phi(X)\right] = \int_{\mathbb{R}}\ \phi(x)\ \mathbb{P}_X(dx),](https://static.techno-science.net/illustration/Definitions/autres/c/c3250b0775e558b2aa3a8e1ff790d166_92bae6d4691c5e00790c90a981017ad2.png)
![\mathbb{P}\left(X\in A\right)=e^{-1}1_A(1)+\int_{A}\ e^{-x}\,1_{[0,1]}(x)\,dx,\qquad\mathbb{E}\left[\phi(X)\right]=e^{-1}\phi(1)+\int_{0}^1\ \phi(x)\ e^{-x}\,dx.](https://static.techno-science.net/illustration/Definitions/autres/0/0769404099bad8f2b248be958c8ec541_41d2d318b99a90da13240c48582d81ab.png)

















































