Loi de probabilité - Définition
La liste des auteurs de cet article est disponible ici.
Exemples de lois discrètes
Une variable aléatoire X est discrète si l'ensemble de ses valeurs possibles est fini ou dénombrable. On dit alors que sa loi est discrète. Pour une définition plus formelle, voir la section "Classification des lois de probabilités sur la droite réelle". Pour la plupart des lois discrètes classiques, les valeurs possibles de X sont des entiers naturels. On définit alors la loi discrète en donnant la probabilité que X prenne chaque valeur entière possible n, soit
-
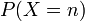
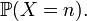
Loi uniforme discrète
La loi uniforme discrète correspond à des événements équiprobables (exemple : lancer de dés, n=6 ) :
Loi de Bernoulli
La loi de Bernoulli correspond à une expérience à deux issues (succès - échec), codées resp. par les valeurs 1, 0, et en général non équiprobables :
-
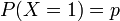
-
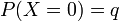
-
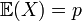
-
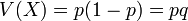
Loi binomiale
C'est la loi du nombre de succès obtenus à l'issue de n épreuves de Bernoulli indépendantes de paramètre p.
-
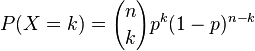
-
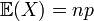
-
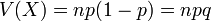
Loi hypergéométrique
On tire simultanément n boules dans une urne contenant pA boules gagnantes et qA boules perdantes (avec q = 1 - p, soit un nombre total de boules valant pA + qA = A). On compte alors le nombre de boules gagnantes extraites et on appelle X la variable aléatoire donnant le nombre de boules gagnantes.
-
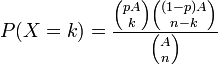
-
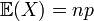
-
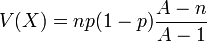
Loi de Poisson
Loi géométrique
On considère une épreuve de Bernoulli dont la probabilité de succès est p et celle d'échec q = 1 - p.
On renouvelle cette épreuve de manière indépendante jusqu'au premier succès. On appelle X la variable aléatoire donnant le rang du premier succès.
-
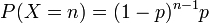
-
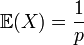
-
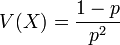
Caractérisation de la loi de probabilité d'une variable aléatoire réelle
En probabilité, il est crucial de pouvoir vérifier que deux variables aléatoires (réelles ou pas) ont la même loi de manière la plus économique possible, or les caractérisations ci-dessus exigent de vérifier des familles d'identités beaucoup trop riches (pour tout borélien B, pour toute fonction borélienne φ ...). Une solution plus ergonomique est fournie par les notions de fonction de répartition, ou de fonction caractéristique.
Caractérisation à l'aide de la fonction de répartition
La loi d'une variable aléatoire réelle est caractérisée par sa fonction de répartition : deux variables aléatoires réelles

Ainsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de boréliens
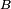
![\scriptstyle\ ]-\infty,x],\](https://static.techno-science.net/illustration/Definitions/autres/1/1711bb012e78b43510de09326a6dd123_d2de886a05c786b59500e894e8e1286c.png)
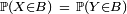
![\scriptstyle\ \mathbb{E}\left[\phi(X)\right]\ =\ \mathbb{E}\left[\phi(Y)\right]](https://static.techno-science.net/illustration/Definitions/autres/0/0c50fd143e72130628f59daf45615b33_7648b8d6dc3c8799e52191006a86156d.png)
Caractérisation à l'aide de la fonction caractéristique
La loi d'une variable aléatoire réelle est caractérisée par sa fonction caractéristique : deux variables aléatoires réelles

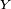
Ainsi il suffit de vérifier l'égalité caractéristique pour une famille réduite de fonctions
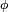
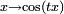
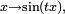

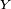
Caractérisation à l'aide de la transformée de Laplace
La loi d'une variable aléatoire réelle positive ou nulle est caractérisée par sa transformée de Laplace : deux variables aléatoires réelles positives ou nulles

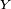
Caractérisation à l'aide de la fonction génératrice
La loi d'une variable aléatoire à valeurs entières positives ou nulles est caractérisée par sa fonction génératrice : deux variables aléatoires à valeurs entières positives ou nulles

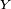
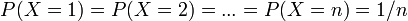
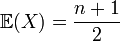
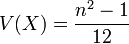
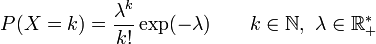
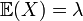
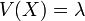
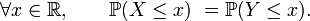
![\forall t\in\mathbb{R},\qquad\mathbb{E}\left[e^{itX}\right]\ = \mathbb{E}\left[e^{itY}\right].](https://static.techno-science.net/illustration/Definitions/autres/0/0327c4d61fbe62656f5ae75fea3dce9e_3132da4e05bcfdbda04c070d546ad39e.png)
![\forall \lambda>0,\qquad\mathbb{E}\left[e^{-\lambda X}\right]\ = \mathbb{E}\left[e^{-\lambda Y}\right].](https://upload.wikimedia.org/math/0/e/0/0e0b5886f280c174ae103b64b3ba583a.png)
![\forall s\in\mathbb{R},\qquad\mathbb{E}\left[s^{X}\right]\ = \mathbb{E}\left[s^{Y}\right].](https://static.techno-science.net/illustration/Definitions/autres/e/e1c22c05e393201d965072b01d2ddebc_46557445cb54195d7b735e9d23a8c5e8.png)

















































