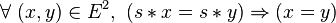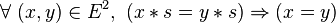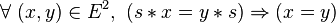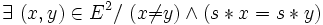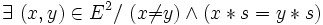Loi de composition interne - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Éléments particuliers
Composé de deux éléments et composé réciproque
Dans un magma ( E,



L'élément y



Certains éléments jouent un rôle particulier en raison de leurs propriétés :
Carrés et dérivés
- un élément

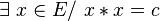
- En sens inverse, tout élément x a un carré unique, noté habituellement « x 2 ».
- Si la loi est notée additivement, le terme de double sera employé de préférence à celui de carré.
- Exemple : dans
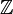
- Exemple : dans
- un élément

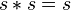
- En d’autres termes, cet élément est son propre carré.
- Exemples :
- tout élément neutre d'une loi est idempotent pour cette loi;
- dans tout ensemble numérique les contenant, 0 et 1 sont les seuls éléments idempotents pour la multiplication.
- Exemples :
- un élément
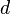
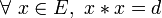
- En d’autres termes, d est le carré de tous les éléments de E. Tout élément dévolutif est idempotent. En effet, il est carré de tout élément de E donc en particulier, il est son propre carré
- Exemple : dans un groupe dont tous les éléments autres que le neutre sont d'ordre deux, l'élément neutre est dévolutif.
Neutres et dérivés
- un élément

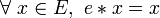
- un élément

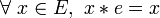
- un élément

-
- Exemple : dans
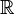
- Exemple : dans
- Tout élément neutre, même unilatère (c’est-à-dire soit à gauche, soit à droite, mais pas les deux), est idempotent.
- un élément


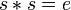
- L’élément neutre est nécessairement involutif.
- Le seul élément involutif et idempotent est l'élément neutre.
- un élément


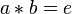


Absorbants et dérivés
- un élément

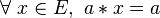
- un élément

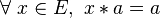
- un élément

-
- Exemple : dans
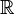
- Exemple : dans
- Tout élément absorbant, même unilatère, est idempotent.
- un élément


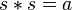
- L’élément absorbant est nécessairement nilpotent...
Centre d'une structure
- un élément

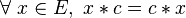
- En d'autres termes, un élément est central si son composé par tout élément se confond avec le réciproque de ce composé.
- Les éléments neutre et absorbant bilatères sont commutatifs.
- On appelle centre de E, et on note Z ( E ), l’ensemble des éléments commutatifs de E.
Réguliers et dérivés
- un élément

- un élément

- un élément

- un élément

- un élément

- un élément

- un élément

- un élément



- Un diviseur de zéro à gauche est irrégulier à gauche;
- un élément



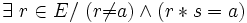
- Un diviseur de zéro à droite est irrégulier à droite;
Paires d'éléments
Des paires d’éléments peuvent aussi présenter des propriétés particulières :
- deux éléments



- ou, en d'autres termes, si leur composé se confond avec son réciproque.
- deux éléments permutables


- - s’il existe un élément neutre

- - et si :
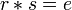
- deux éléments permutables


- - s’il existe un élément absorbant

- - si aucun des deux éléments n’est égal à

- - et si :
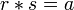
- Les diviseurs de zéro sont irréguliers. Les éléments nilpotents autres que l’élément absorbant sont des diviseurs de zéro.
Exemple: pour les entiers relatifs, 0 est neutre pour l’addition, absorbant pour la multiplication, et neutre à droite pour la soustraction.