Loi de Rayleigh - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Lien avec d'autres distributions continues
- R˜Rayleigh(σ) suit la loi de Rayleigh si
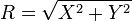
- Si R˜Rayleigh(1) , alors R2 suit la loi du χ² avec 2 degrés de liberté:
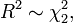
- Si X suit une loi exponentielle
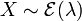
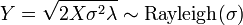
- Si Ri˜Rayleigh(σ), et si les Ri forment une suite de variables indépendantes, alors
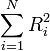
![[Y=\sum_{i=1}^N R_i^2] \sim \Gamma(N,2\sigma^2)](https://static.techno-science.net/illustration/Definitions/autres/b/b2a73fb8d83427b643055fabc41f2f14_2a22bea8c6d52cc7a255855ad51942f7.png)
- La loi de Rice est une généralisation de la loi de Rayleigh.
![[Y=\sum_{i=1}^N R_i^2] \sim \Gamma(N,2\sigma^2)](https://static.techno-science.net/illustrationWebp/Definitions/autres/b/b2a73fb8d83427b643055fabc41f2f14_2a22bea8c6d52cc7a255855ad51942f7.png)
