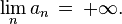Loi de Poisson - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Poisson | |
|---|---|
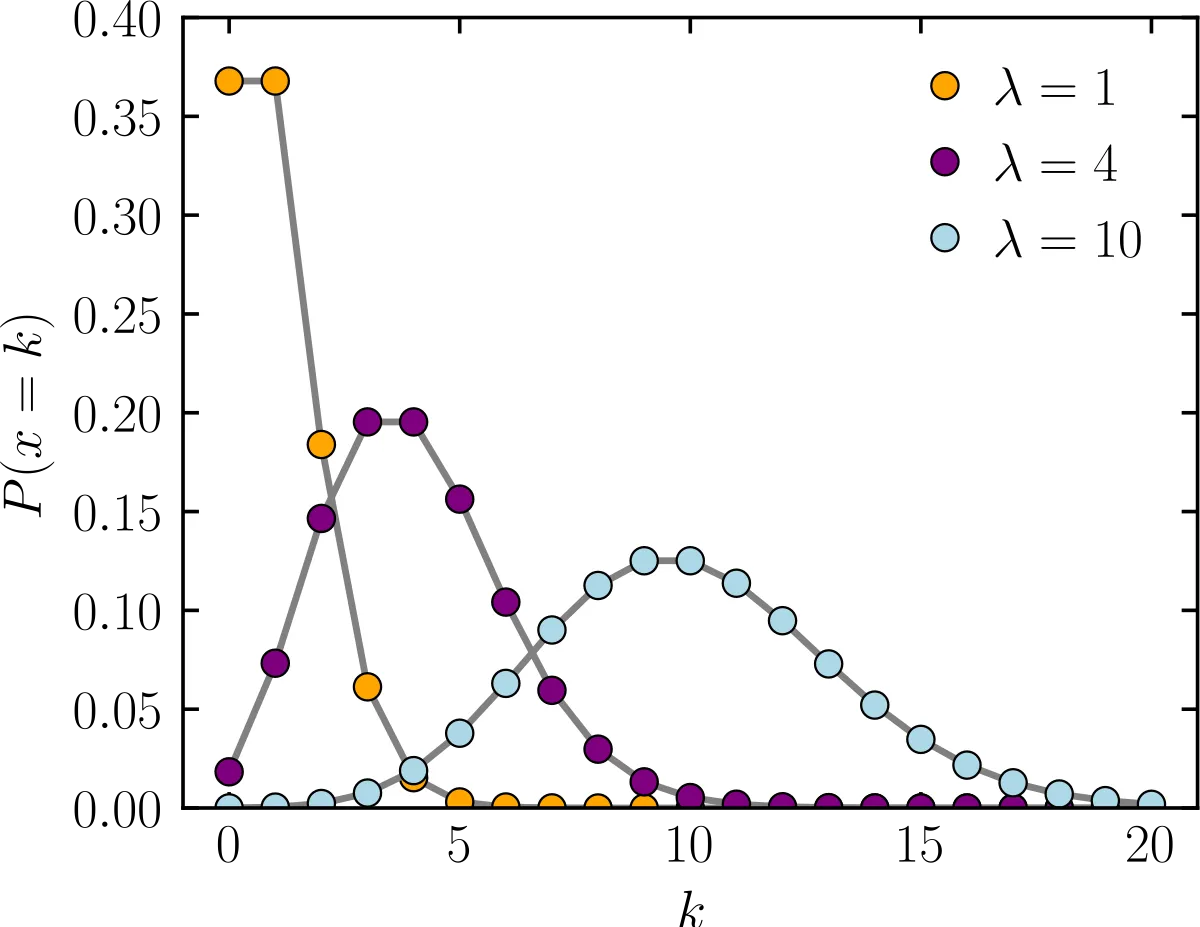
L'axe horizontal est l'indice k. La fonction est seulement définie pour les valeurs entières de k. | |

L'axe horizontal est l'indice k. La fonction de répartition est seulement discontinue pour les valeurs entières de k. | |
| | |
| Paramètres |
|
| Support |
|
| Densité de probabilité (fonction de masse) |
|
| Fonction de répartition |
(où Γ(x,y) est la Fonction gamma incomplète) |
| Espérance |
|
| Médiane (centre) |
|
| Mode |
|
| Variance |
|
| Asymétrie (statistique) |
|
| Kurtosis (non-normalisé) |
|
| Entropie |
![\lambda[1\!-\!\log(\lambda)]\!+\!e^{-\lambda}\sum_{k=0}^\infty \frac{\lambda^k\log(k!)}{k!}.](https://static.techno-science.net/illustration/Definitions/autres/8/86583b21ed9852b77ef35b43a57b2b54_1c612368f73b332884162d0bedd295a3.png)
Pour λ grand :
|
| Fonction génératrice des moments |
|
| Fonction caractéristique |
|
| modifier | |
En théorie des probabilités et en statistiques, la loi de Poisson est une loi de probabilité discrète qui décrit le comportement du nombre d'évènements se produisant dans un laps de temps fixé, si ces évènements se produisent avec une fréquence moyenne connue et indépendamment du temps écoulé depuis l'évènement précédent. La loi de Poisson est également pertinente pour décrire le nombre d'évènements dans d'autres types d'intervalles, spatiaux plutôt que temporels, comme des segments, surfaces ou volumes.
La loi de Poisson a été introduite en 1838 par Siméon-Denis Poisson (1781–1840), dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile [1]. Le sujet principal de cet ouvrage consiste en certaines variables aléatoires N qui dénombrent, entre autres choses, le nombre d'occurrences (parfois appelées “arrivées”) qui prennent place pendant un laps de temps de longueur donnée.
Si le nombre moyen d'occurrences dans cet intervalle est λ, alors la probabilité qu'il existe exactement k occurrences (k étant un entier naturel, k = 0, 1, 2, ...) est
où
- e est la base de l'exponentielle (2,718...)
- k! est la factorielle de k
- λ est un nombre réel strictement positif.
On dit alors que X suit la loi de Poisson de paramètre λ.
Par exemple, si un certain type d'évènements se produit en moyenne 4 fois par minute, pour étudier le nombre d'évènements se produisant dans un laps de temps de 10 minutes, on choisit comme modèle une loi de Poisson de paramètre λ = 10× 4 = 40.
Calcul de p(k)
Ce calcul peut se faire de manière déductive en travaillant sur une loi binomiale de paramètres (T; λ/T). Pour T grand, on démontre que la loi binomiale converge vers la loi de Poisson.
Il peut aussi se faire de manière inductive en étudiant sur l'intervalle [0; T] les fonctions Fk(t) = probabilité que l'événement se produise k fois sur l'intervalle de temps [0 ; t]. En utilisant la récurrence et du calcul différentiel, on parvient à retrouver les formules précédentes.
Domaine d'application
Le domaine d'application de la loi de Poisson a été longtemps limité à celui des événements rares comme les suicides d'enfants, les arrivées de bateaux dans un port ou les accidents dus aux coups de pied de cheval dans les armées (étude de Ladislaus Bortkiewicz).
Mais depuis quelques décennies son champ d'application s'est considérablement élargi. Actuellement, on l'utilise beaucoup dans les télécommunications (pour compter le nombre de communications dans un intervalle de temps donné), le contrôle de qualité statistique, la description de certains phénomènes liés à la désintégration radioactive (la désintégration des noyaux radioactifs suivant, par ailleurs, une loi exponentielle de paramètre noté aussi lambda), la biologie (mutations), la météorologie, la finance pour modéliser la probabilité de défaut d'un crédit…
Lien avec la loi de Bernoulli
Le décompte des évènements rares se fait souvent au travers d'une somme de variables de Bernoulli, la rareté des évènements se traduisant par le fait que les paramètres de ces variables de Bernoulli sont petits (ainsi, la probabilité que chaque évènement survienne est faible). Le lien entre la loi de Poisson et les évènements rares peut alors s'énoncer ainsi :
Paradigme de Poisson — La somme Sn d'un grand nombre de variables de Bernoulli indépendantes de petit paramètre suit approximativement la loi de Poisson de paramètre
![\scriptstyle\ \mathbb{E}[S_n]. \](https://static.techno-science.net/illustration/Definitions/autres/5/5727907d43850533ffb9dab459c30599_fcd46d89adba9157b1d4167ce679b4e5.png)
L'inégalité de Le Cam précise le paradigme de Poisson : soit

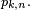
Inégalité de Le Cam — Pour tout ensemble A d'entiers naturels,

En particulier, si les deux conditions suivantes sont réunies :
alors Sn converge en loi vers la loi de Poisson de paramètre λ.
Dans l'énoncé du paradigme de Poisson, on fait deux hypothèses (vagues) sur les termes d'une somme Sn de variables de Bernoulli :
- les paramètres des variables de Bernoulli sont petits ; or les deux conditions ci-dessus entrainent que
- il y a un grands nombre de termes ; or les deux conditions ci-dessus entrainent que
- Ce paradigme reste pertinent, dans certaines conditions, si l'on relaxe l'hypothèse d' indépendance.
- Un exemple frappant est le nombre de points fixes d'une permutation tirée au hasard.
- Un autre exemple est le nombre de points isolés du graphe aléatoire, dont la convergence vers la loi de Poisson a permis à Erdös et Rényi de démontrer, en 1960, le théorème double-exponentiel.
- Le cas particulier an=n, pk,n=λ/n, λn=λ, de l'inégalité de Le Cam, précise la rapidité de convergence de la loi binomiale de paramètres n et λ/n vers la loi de Poisson de paramètre λ.
![\lambda \in ]0,\infty[](https://static.techno-science.net/illustration/Definitions/autres/9/99524d2535c53cce0cea175e93d127cc_264ab019f41fae8794f6160b9e6c069b.png)



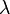







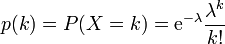
![S_n=\sum_{k=1}^{a_n}\,X_{k,n}\quad\text{et}\quad\lambda_n\ =\ \mathbb{E}[S_n]=\sum_{k=1}^{a_n}\,p_{k,n}.\](https://static.techno-science.net/illustration/Definitions/autres/6/6541a45bb94abcc6be00442dca3ac601_a96e916a4013b7feeebfcec584b249a5.png)