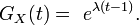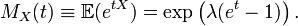Loi de Poisson - Définition
La liste des auteurs de cet article est disponible ici.
Espérance, variance, écart type, fonctions génératrices
- L'espérance d'une loi de Poisson est λ.
- La variance d'une loi de Poisson est également λ.
- Son écart type est donc
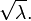
- La fonction génératrice de la loi de Poisson est
- La fonction génératrice des moments d'une loi de Poisson est
Espérance
Si


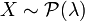
Alors, on a par définition que
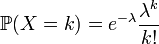
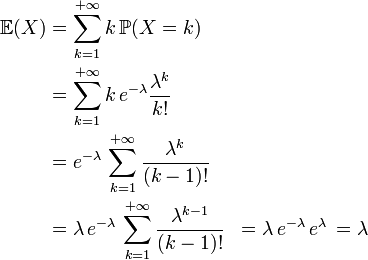
Dans la dernière ligne, on reconnaît le développement en série entière de
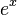
Variance
![\begin{align}V(X) &= \mathbb{E}(X^2) - ( \mathbb{E}(X) ) ^2\\ &= \sum_{k=1}^{+{\infty}}k^2\,\mathbb{P}(X=k) - \lambda^2\\ &= \sum_{k=1}^{+{\infty}}k^2\,e^{-\lambda}\frac{\lambda^k}{k!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \sum_{k=1}^{+{\infty}}\,\frac{k\lambda^{k-1}}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \sum_{k=1}^{+{\infty}}\,\frac{d}{d\lambda}\frac{\lambda^k}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda} \sum_{k=1}^{+{\infty}}\,\frac{\lambda^k}{(k-1)!} - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\sum_{k=1}^{+{\infty}}\,\frac{\lambda^{k-1}}{(k-1)!}] - \lambda^2\\ &= \lambda\,e^{-\lambda} \frac{d}{d\lambda}[\lambda\,e^{\lambda}] - \lambda^2 \qquad \qquad \text{ car } \exp(x) = \sum_{n = 0}^{+\infty} {x^n \over n!}\\ &= \lambda\,e^{-\lambda}(\lambda+1)\,e^{\lambda} - \lambda^2\\ &= \lambda\,(\lambda+1) - \lambda^2\\ &= \lambda\,\end{align}](https://static.techno-science.net/illustration/Definitions/autres/0/0f02676f4af228acd87254173d7c5581_3393f7c1eab3ee19457ccebbd75ee675.png)
Fonction génératrice
La fonction génératrice d'une variable aléatoire X est définie par
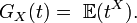
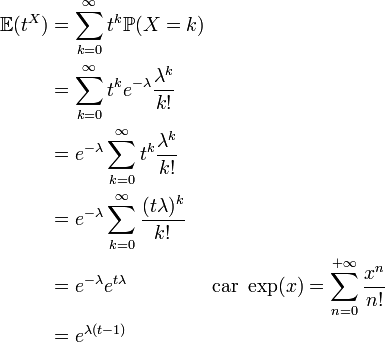
Fonction génératrice des moments
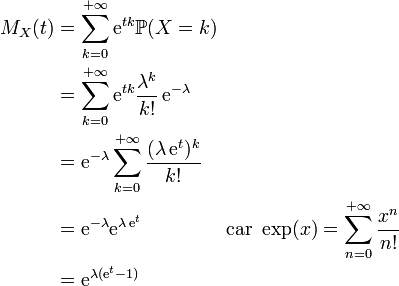
Stabilité de la loi de Poisson par la somme
Si X et Y sont deux variables aléatoires indépendantes qui suivent des lois de Poisson de paramètres λ et μ, alors X+Y est une variable aléatoire qui suit la loi de Poisson de paramètre λ + μ.
Théorème — Si
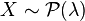
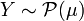
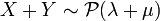
La démonstration est faite ici par la fonction génératrice des moments. On sait en effet que MX + Y(t) = MX(t)MY(t) par indépendance de X et Y et que la fonction génératrice des moments détermine univoquement la loi.
En partant du résultat démontré : MX(t) = exp(λ(et − 1)),
on calcule: MX + Y(t) = MX(t)MY(t) = exp(λ(et − 1))exp(μ(et − 1)) = exp(λ(et − 1) + μ(et − 1)) = exp((λ + μ)(et − 1))
Le résultat MX + Y(t) = exp((λ + μ)(et − 1)) est simplement la fonction génératrice des moments d'une loi de Poison de paramètre λ + μDiagrammes en bâtons
Comme toute loi de probabilité discrète, une loi de Poisson peut être représentée par un diagramme en bâtons. Ci-dessous sont représentés les diagrammes en bâtons des lois de Poisson de paramètres 1, 2 et 5.
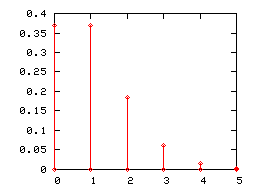
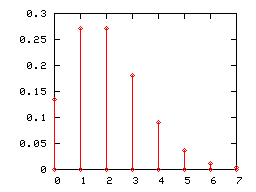
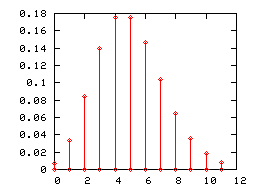
Lorsque le paramètre λ de la loi de Poisson devient grand, (pratiquement lorsqu'il est supérieur à 5), son diagramme en bâton est correctement approché par l'histogramme d'une loi normale d'espérance et de variance égales à λ (l'intervalle de classe étant égal à l'unité). Cette convergence était mise à profit, avant que les moyens informatiques ne se généralisent, pour utiliser la loi normale en lieu et place de la loi de Poisson dans certains tests.
En littérature
Dans le roman de Thomas Pynchon, L'Arc-en-ciel de la gravité, un des personnages, le statisticien Roger Mexico, utilise la loi de Poisson pour cartographier les zones d'impact des fusées allemandes V2 sur la ville de Londres durant la bataille d'Angleterre.