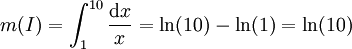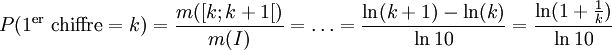Loi de Benford - Définition

Application

La loi de Benford est utilisée aux États-Unis, ainsi que dans d'autres pays, dont la France, pour détecter des fraudes fiscales, suite aux idées exposées en 1972 par Hal Varian. Les premiers chiffres significatifs 5 et 6 prédominent nettement dans les données falsifiées : 40 % pour les 5 et plus de 20 % pour les 6. Pour proposer un modèle de prédiction d'indice boursier, il convient d'inclure un test de cohérence car la loi de Benford ne fait pas de distinction entre les nombres 20 et 200 000 : ces deux nombres ayant 2 et 0 comme chiffres significatifs.

Ébauche de démonstration

Choisissons un nombre réel strictement positif appartenant à un intervalle I.

On cherche la probabilité de son premier chiffre non nul, indépendamment de toute autre caractéristique.

Cela correspond à la recherche d'une mesure m sur l'ensemble I, supposé mesurable, avec :

1. 
2. 
3. 
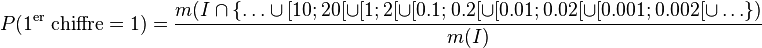
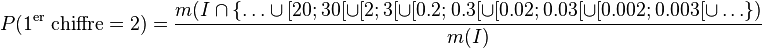
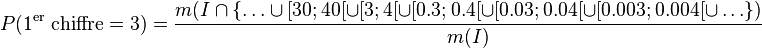
4. etc.

On suppose que I est construit comme une union de produits de l'intervalle [1;10[ par des réels a_i > 0 ; c'est-à-dire : I = ∪ a_i × [1;10[ pour des a_i > 0. Donc, on travaille dans le groupe multiplicatif des réels strictement positifs (car c'est ainsi que la topologie de ce groupe est construite).

L'ensemble des réels strictement positifs muni de la multiplication étant un groupe topologique séparable et localement compact, il existe une et une seule mesure (à un coefficient multiplicateur près) qui soit invariante par la loi de groupe : la mesure de Haar du groupe.

Cette mesure est .

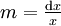
Prenons I = [1;10[, on a :

Et on a :

Comme la mesure m est invariante par le produit, en prenant I = ∪ a_i × [1;10[ avec a_i = 10ⁿ , on arrive au même résultat (on peut aussi le vérifier par le calcul).

Ébauche faite à partir d'un travail exposé sur le site de l'Université Paris 5. Il manque dans ces deux exposés un argument convaincant sur la nécessité d'utiliser la mesure de Haar.

Explication

Les explications les plus classiques supposent que les suites habituelles admettent des caractéristiques particulières.

La forme précise de la loi de Benford peut par exemple être expliquée si l'on admet que les logarithmes des nombres sont uniformément distribués. Cela signifie qu'un nombre a autant de chances d'être entre 100 et 1 000 (logarithme entre 2 et 3) qu'il a de chances de se trouver entre 10 000 et 100 000 (logarithme entre 4 et 5). Pour de nombreux ensembles de nombres, et tout particulièrement ceux qui croissent exponentiellement, comme les chiffres d'affaire d'entreprises et les cours de bourse, cette supposition est raisonnable.

On peut en particulier l'appuyer par le raisonnement suivant : si une loi générale de distribution des nombres existe, elle doit être indépendante d'un choix d'unité (donc rester valable après multiplication par une constante) et d'un choix de base. L'équidistribution des logarithmes satisfait ces conditions, et est donc un candidat crédible.

Si une variable résulte de la multiplication entre elles d'un grand nombre de variables indépendantes, alors elle suit à peu près la loi de Benford (exactement à la limite).

Mais ces explications sont à la fois spécifiques (à un certain type de données) et spéculatives (pourquoi supposer que les facteurs agissent multiplicativement ou que le logarithme suit une loi uniforme ?). Récemment, Gauvrit et Delahaye ont proposé une explication plus simple et générale de la loi de Benford. Selon les chercheurs, c'est le caractère étalé et régulier de la plupart des variables utilisées qui explique la loi de Benford. Ils suggèrent d'ailleurs qu'un équivalent de cette loi, fondé sur d'autres fonctions que le logarithme, fonctionnerait tout aussi bien.

Cette étrange loi a reçu récemment une explication grâce à Jean-Paul Delahaye et Nicolas Gauvrit : « Dès que des nombres issus de phénomènes naturels, économiques ou mathématiques sont étalés sur plusieurs ordres de grandeur de manière à peu près régulière, alors leur répartition suit globalement cette loi. ».