Logique - Définition

Notions élémentaires de logique formelle

Un langage logique est défini par une syntaxe, c'est-à-dire un système de symboles et de règles pour les combiner sous formes de formules. De plus, une sémantique est associée au langage. Elle permet de l'interpréter, c'est-à-dire d'attacher à ces formules ainsi qu'aux symboles une signification. Un système de déduction permet de raisonner en construisant des démonstrations.

La logique comprend classiquement :

• la logique des propositions (aussi appelée calcul des propositions),
• la logique des prédicats.

Considérons un langage logique. Ce dernier est soit :

• un langage propositionnel, on parle alors de logique des propositions,
• un langage contenant des notations pour des entités avec des quantifications sur ces entités, on parle alors de logique des prédicats.

Syntaxes

La syntaxe de la logique des propositions est fondée sur des variables de propositions appelées également atomes que nous notons avec des lettres minuscules (p, q, r, s, etc.). Ces symboles représentent des propositions sur lesquelles on ne porte pas de jugement vis-à-vis de leur vérité : elles peuvent être soit vraies, soit fausses, mais on peut aussi ne rien vouloir dire sur leur statut. Ces variables sont combinées au moyen de connecteurs logiques qui sont, par exemple :

1. le connecteur binaire disjonctif (ou), de symbole: ∨ ;
2. le connecteur binaire conjonctif (et), de symbole: ∧ ;
3. le connecteur binaire de l'implication, de symbole: → ;
4. le connecteur monadique de la négation (non), de symbole: ¬.

Ces variables forment alors des formules complexes.

La syntaxe de la logique du deuxième ordre, contrairement à celle du premier ordre, considère d'une part les termes qui représentent les objets étudiés, et d'autre part les formules qui sont des propriétés sur ces objets. Dans la suite nous noterons V l'ensemble des variables (x, y, z...), F l'ensemble des symboles de fonctions (f, g...) et P l'ensemble des symboles de prédicats (P, Q...). On dispose également d'une application dite d'arité m.

Qu'en est-il de la signification d'une formule ? C'est l'objet de la sémantique. Là encore, elle diffère selon le langage envisagé.

En logique traditionnelle (appelée aussi classique), une formule est soit vraie soit fausse. Plus formellement, l'ensemble des valeurs de vérité est un ensemble B de deux booléens : le vrai et le faux. La signification des connecteurs est définie à l'aide de fonctions de booléens vers des booléens. Ces fonctions peuvent être représentées sous la forme de table de vérité.

La signification d'une formule dépend donc de la valeur de vérité de ses variables. On parle d'interprétation ou d'affectation. Toutefois, il est difficile, au sens de la complexité algorithmique, d'utiliser la sémantique pour décider si une formule est satisfaisante (ou non) voire valide (ou non). Il faudrait pour cela pouvoir énumérer toutes les interprétations. Leur nombre est exponentiel.

Une alternative à la sémantique consiste à examiner les preuves bien formées et à considérer leurs conclusions. Cela se fait dans un système de déduction. Un système de déduction est un couple (A, R), où A est un ensemble de formules appelées axiomes et R un ensemble de règles d'inférence, c'est-à-dire de relations entre des ensembles de formules (les prémisses) et des formules (la conclusion).

On appelle dérivation à partir d'un ensemble donné d'hypothèses une suite non vide de formules qui sont : soit des axiomes, soit des formules déduites des formules précédentes de la suite.

Une démonstration d'une formule φ à partir d'un ensemble de formules Γ est une dérivation à partir de Γ dont la dernière formule est φ.

Quantification

On introduit essentiellement deux quantificateurs dans la logique moderne :

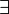• (il existe au moins un), appelé quantificateur existentiel.

• (pour tout), appelé quantificateur universel.

Grâce à la négation, les quantificateurs existentiels et universels jouent des rôles duaux et donc, en logique classique, on peut fonder le calcul des prédicats sur un seul quantificateur.

Égalité

Un prédicat binaire, que l'on appelle égalité, énonce le fait que deux termes sont égaux quand ils représentent le même objet. Il est géré par des axiomes ou schémas d'axiomes spécifiques. Cependant parmi les prédicats binaires c'est un prédicat très particulier, dont l'interprétation usuelle n'est pas seulement contrainte par ses propriétés énoncées par les axiomes : en particulier il n'y a usuellement qu'un prédicat d'égalité possible par modèle, celui qui correspond à l'interprétation attendue (l'identité). Son adjonction à la théorie préserve certaines bonnes propriétés comme le théorème de complétude du calcul des prédicats classique. On considère donc très souvent que l'égalité fait partie de la logique de base et l'on étudie alors le calcul des prédicats égalitaire.

Dans une théorie qui contient l'égalité, un quantificateur, qui peut être défini à partir des quantificateurs précédents et de l'égalité, est souvent introduit :

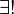• (il existe un et un seul).

D'autres quantificateurs peuvent être introduits en calcul des prédicats égalitaires (il existe au plus un objet vérifiant telle propriété, il existe deux objets ...), mais des quantificateurs utiles en mathématiques, comme « il existe une infinité ... » ou « il existe un nombre fini ... » ne peuvent s'y représenter et nécessitent d'autres axiomes (comme ceux de la théorie des ensembles).