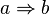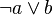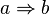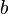Logique intuitionniste - Définition

Introduction

L'intuitionnisme est une position philosophique vis-à-vis des mathématiques proposée par le mathématicien hollandais Luitzen Egbertus Jan Brouwer comme une alternative à l'approche dite classique. Elle a été ensuite formalisée, sous le nom de logique intuitionniste, par ses élèves V. Glivenko et Arend Heyting. Kurt Gödel a montré que l'on pouvait représenter la logique classique dans la logique intuitionniste, corroborant le fait que la logique intuitionniste n'est pas une logique à part, mais fait bien partie de la Logique. Gerhard Gentzen en a formalisé les règles de déduction dans le cadre de la déduction naturelle.

Les travaux récents, notamment la correspondance de Curry-Howard, lui ont donné un statut central dans la logique et dans l'informatique, en faisant d'elle historiquement la première des logiques constructives. Des travaux la concernant, effectués par Gödel et Andreï Kolmogorov au sujet de la « Non-non interprétation » (interprétation de la double négation) ont ouvert la porte de l’interprétation de la logique classique dans les termes de la logique intuitionniste. L'étude de la logique intuitionniste est la clé pour bien comprendre la logique classique et ses subtilités.

Approche informelle

Brouwer a fondé l'intuitionnisme comme une position philosophique vis-à-vis des mathématiques ; cela l'a conduit à rejeter certaines formes du raisonnement mathématique traditionnel, qu'il jugeait contre-intuitives. En fait, il refusait deux principes.

• Le tiers exclu, qui consiste à dire qu'étant donnée une proposition φ, soit on a φ, soit on a non(φ), formellement . A titre d'exemple, il rejetait le raisonnement suivant :

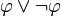
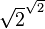
« Il existe des nombres irrationnels a et b, tels que a^b est un nombre rationnel. En effet, on sait que la racine carrée de deux est irrationnelle, et 2 est évidemment rationnel. En notant la proposition «  est rationnel », on pourrait alors dire :

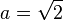
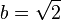
si est vrai alors les irrationnels et conviennent,

si est faux alors les irrationnels et conviennent (l'irrationalité de a étant l’hypothèse ), puisque est rationnel ».

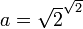
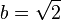
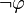
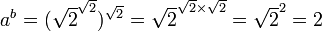
La critique de cette démonstration est qu'elle n'est pas constructive : de par son utilisation du tiers exclu, elle n'exhibe pas une solution explicite, mais démontre seulement l'existence d'un couple-solution sans pouvoir préciser lequel (puisqu'on ne sait pas si est vrai ou faux). En fait, le théorème de Gelfond-Schneider permet de montrer que est irrationnel et que c'est le a qu'il faut choisir, mais la démonstration fondée sur le tiers exclu ne le dit pas.

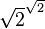
• L'existentiel non constructif. Brouwer veut que quand un mathématicien affirme il existe x tel que x est P, que l'on écrirait formellement , il donne aussi un moyen de construire x qui satisfait P.

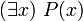
Brouwer a prôné une mathématique qui rejetterait le tiers exclu et n'accepterait que l'existentiel constructif. Cette attitude a été assez violemment critiquée par des mathématiciens comme David Hilbert tandis que d'autres comme Hermann Weyl y ont souscrit. Une fois formalisée, trois faits font de la logique intuitionniste une logique à part entière : l'existence de modèles qui font d'elle un système complet de déduction, la découverte de son contenu calculatoire, connu sous le nom de correspondance de Curry-Howard, enfin le fait qu'elle est une logique modale. La logique intuitionniste n'a donc rien d'exotique. Allant plus loin, le logicien Jean-Yves Girard a proposé une logique plus faible que la logique intuitionniste, qu'il a appelée la logique linéaire, qui se trouve à la base de toute logique et qui permet de mieux comprendre la logique intuitionniste en particulier.

La logique intuitionniste revisite aussi le concept d'implication. L'implication n'est plus l'implication matérielle . Quand un mathématicien intuitionniste affirme , il veut dire qu'il fournit un procédé de « construction » d'une démonstration de à partir d'une démonstration de . Ceci est d'ailleurs la clé du contenu calculatoire de la logique intuitionniste.