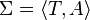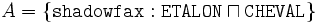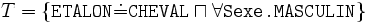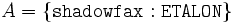Logique de description - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Les logiques de description aussi appelé logiques descriptives (LDs) sont une famille de langages de représentation de connaissance qui peuvent être utilisés pour représenter la connaissance terminologique d'un domaine d'application d'une manière formelle et structurée. Le nom de logique de description se rapporte, d'une part à la description de concepts utilisée pour décrire un domaine et d'autre part à la sémantique basée sur la logique qui peut être donnée par une transcription en logique des prédicats du premier ordre. La logique de description a été développée comme une extension des frames et des réseaux sémantiques, qui ne possédaient pas de sémantique formelle basée sur la logique.
Origines et applications des logiques de description
Les logiques de description ont été conçues à partir des réseaux sémantiques de Quillian () qui sont des graphes orientés étiquetés auxquels on associe des concepts aux nœuds et des relations aux arcs, et de la sémantique des cadres de Minsky () où l'on a des concepts représentés par des cadres qui sont caractérisés par un certain nombre d'attributs (appelés aussi slots) qui contiennent de l'information sur leur contenu.
Les logiques de description forment une famille de langages de représentation de connaissance qui peuvent être utilisées pour représenter la connaissance terminologique d'un domaine d'application d'une façon structurée et formelle. Le nom « logique de description » peut être interprété de deux manières. D'une part ces langages ont été élaborés pour écrire la « description » des concepts pertinents d'un domaine d'application. D'autre part, une caractéristique cruciale de ces langages est qu'ils ont une sémantique formelle définie en logique du premier ordre (à la différence des propositions précédentes comme les cadres de Minsky). Dans ce sens, nous pouvons dire que les LDs ont une sémantique « descriptive » formelle.
Les logiques de description sont utilisées pour de nombreuses applications (voir International Workshop on Description Logics et Workshop on Applications of Description Logics). Sans être exhaustif, nous pouvons dire que ces applications font partie des domaines suivants :
- le web sémantique (e.g., représentation d'ontologies, et recherche d'information basée sur la logique)
- médecine/bio-informatique (e.g., représenter et gérer des ontologies biomédicales)
- traitement automatique des langues et représentation de la connaissance
- Ingénierie de processus (e.g., représenter des descriptions de service)
- Ingénierie de la connaissance (e.g., représenter des ontologies)
- Ingénierie logicielle (e.g., représenter la sémantique des diagrammes de classe UML)
Les tâches de raisonnement
En LD, l'expression raisonnement sur la T-Box fait référence à la capacité de réaliser des inférences depuis une base de connaissance
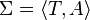
Définition 4 :
- Soit Σ une base de connaissances,
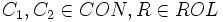
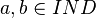
- Subsomption,
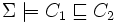
Vérifie si pour toutes les interprétations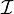
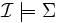
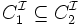
- Vérification d'instance,
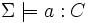
Vérifie si pour toutes les interprétations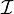
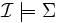
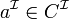
- Vérification de relations
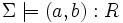
Vérifie si pour toutes les interprétations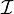
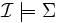
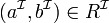
- Cohérence de concept,
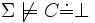
Vérifie si pour toutes les interprétations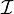
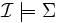
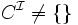
- Cohérence de la base de connaissances,
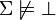
Vérifie s'il existe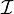
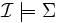
- Subsomption,
Les tâches de déduction de base peuvent être utilisées pour définir des tâches plus complexes. En particulier:
- Recherche : étant donné un concept, trouver les individus mentionnés dans la base de connaissance qui sont des instances de ce concept.
- Réalisation : étant donné un individu mentionné dans la base de connaissance, trouver le concept le plus spécifique, en accord avec les relations de subsomption, duquel l'individu est une instance.
La saturation de la A-Box sert à compléter les informations de la A-Box en accord avec les connaissances de la T-Box, on obtient donc: Définition 5 :
- Étant donné une base de connaissance
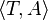
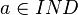
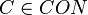
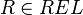
- l'assertion a:C si et seulement si
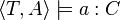
- l'assertion (a,b):R si et seulement si
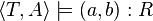
- l'assertion a:C si et seulement si
Exemple
- Soit Σ une base de connaissance
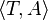
-
La formule de T dit que les chevaux de sexe masculin sont des étalons, et la formule de A dit que le cheval shadowfax est un étalon. La sémantique formelle que nous donnons dans la définition 3 nous permet de vérifier que Σ a au moins un modèle (i.e., il est cohérent). Et à partir de Σ nous pouvons déduire plusieurs informations comme, par exemple, que le concept
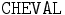
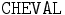
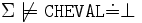
Notons qu'à cause des limitations syntaxiques dans la définition de base des assertions, il n'est pas possible de représenter les implications fortes (qui proviennent de
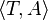
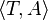
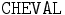

Avec