Liste de critères de divisibilité - Critère de divisibilité par 16

Critère de divisibilité par 16

Un nombre est divisible par 16 si le nombre formé par ses 4 derniers chiffres est divisible par 16.

Exemple

2007557744 est divisible par 16 car 7744 est divisible par 16.

Critère de divisibilité par 15

Un nombre est divisible par 15 s'il est à la fois divisible par 3 et par 5

Critère de divisibilité par 18

Un nombre est divisible par 18 s’il est divisible à la fois par 9 et par 2.

Critère de divisibilité par 17

Lemme de divisibilité par 17

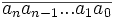
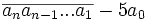
Le nombre $\overline{a_n a_{n-1}...a_1 a_0}$ est divisible par 17 si et seulement si $\overline{a_n a_{n-1}...a_1 } - 5a_0$ est divisible par 17.

Il suffit de répéter l'opération ci-dessus et de vérifier que le résultat final est un multiple de 17.

Soit le nombre 3723. On a
372 – 5 × 3 = 357
35 – 5 × 7 = 0

Nous trouvons un résultat divisible par 17 donc 3723 est divisible par 17.

Critère pour un grand nombre

Supposons que l'on veuille savoir si un nombre contenant un très grand nombre de chiffres est divisible par 17.

Il suffit de séparer ce nombre par tranche de 8 chiffres en partant des unités et d'insérer alternativement des - et des + entre les tranches à partir du début du nombre en commençant par un -.

On effectue l'opération ainsi écrite et si le résultat est divisible par 17, alors le grand nombre considéré est divisible par 17.

Bien sur pour voir si le résultat de l'opération précédente est divisible par 17, on peut utiliser le début de ce paragraphe.

Exemple

Soit le nombre 416521368699986479153682401.

On le sépare par tranche de 8 à partir des unités.

416 | 52136869 | 99864791 | 53682401.

On intercale alternativement des + et des - à partir du début en commençant par un -.

416 - 52136869 + 99864791 - 53682401.

On effectue l'opération ainsi écrite.

416 - 52136869 + 99864791 - 53682401 = -5954063

Le résultat étant négatif, on prend la valeur absolue 5954063

On regarde si 5954063 est divisible par 17 à l'aide du lemme de divisibilité par 17.

595406 - 5×3 = 595391

59539 - 5×1 = 59534

5953 - 5×4 = 5933

593 - 5×3 = 578

57 - 5×8 = 17

Nous obtenons un résultat divisible par 17 donc 416521368699986479153682401 est divisible par 17.

Critère de divisibilité par 20

Un nombre est divisible par 20 si le chiffre des unités est 0 et si le chiffre des dizaines est pair.

Critère de divisibilité par 19

Lemme de divisibilité par 19

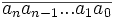
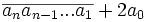
Le nombre $\overline{a_n a_{n-1}...a_1 a_0}$ est divisible par 19 si et seulement si $\overline{a_n a_{n-1}...a_1 } + 2a_0$ est divisible par 19.

Exemples

247 est divisible par 19 car

24 + 2 x 7 = 38

et 38 est divisible par 19.

Critère pour un grand nombre

Pour savoir si un nombre est divisible par 19, Il suffit de séparer ce nombre par tranche de 9 chiffres en partant des unités et d'insérer alternativement des - et des + entre les tranches à partir du début du nombre en commençant par un -. On effectue l'opération ainsi écrite et si le résultat est divisible par 19, alors le nombre considéré est divisible par 19.

Exemples

Soit le nombre 48822138835949515214962479.

On le sépare par tranche de neuf chiffres à partir des unités.

48822138 | 835949515 | 214962479.

On intercale alternativement des + et des - à partir du début en commençant par un -.

48822138 - 835949515 + 214962479

On effectue l'opération ainsi écrite.

48822138 - 835949515 + 214962479 = -572164898

Le résultat n'ayant que 9 chiffres, on vérifie aisément à l'aide d'une calculatrice que 572164898 est divisible par 19 (alors que ce n'était pas possible au départ avec le nombre de 26 chiffres sur la plupart des calculatrices) donc 48822138835949515214962479 est divisible par 19.