Liste de critères de divisibilité - Définition
La liste des auteurs de cet article est disponible ici.
Critère de divisibilité par 12
Un nombre est divisible par 12 s'il est divisible par 3 et par 4.
Exemple
Soit le nombre 3085755924.
Il satisfait au critère de divisibilité par 3 car 3 + 0 + 8 + 5 + 7 + 5 + 5 + 9 + 2 + 4 = 48 qui est divisible par 3.
Il satisfait au critère de divisibilité par 4 car Il se termine par 24 qui est divisible par 4
Par conséquent 3085755924 est divisible par 12.
Critère de divisibilité par 11
Première méthode
Pour déterminer si un nombre N est divisible par 11 :
- on calcule la somme A des chiffres en position impaire ;
- on calcule la somme B des chiffres en position paire ;
N est divisible par 11 si et seulement si la différence A – B (ou B – A) est divisible par 11.
Cela revient à effectuer la somme alternée de ses chiffres.
Exemple
Considérons le nombre 19 382.
- A = 1 + 3 + 2 = 6
- B = 9 + 8 = 17
- B – A = 17 – 6 = 11
Nous trouvons un résultat divisible par 11, donc 19 382 est divisible par 11.
Deuxième méthode
On sépare le nombre par tranche de deux chiffres à partir des unités en intercalant des + et on effectue l'opération obtenue. Si le résultat est divisible par 11 alors le nombre de départ est divisible par 11.
Exemple
Reprenons l'exemple précédent 19382, on obtient :
- 1 + 93 + 82 = 176
Comme le résultat a plus de deux chiffres, on recommence :
- 1 + 76 = 77
77 est divisible par 11 donc 19 382 est divisible par 11 d'après la propriété.
« Mini-critère »
Si un nombre de trois chiffres a son chiffre du milieu égal à la somme des deux chiffres extrêmes et que cette somme est inférieure à 9 alors il est divisible par 11.
Exemples
374 est divisible par 11 car 3 + 4 = 7 on obtient 374 = 11 x 34.
Attention : c'est un critère de divisibilité mais pas de non-divisibilité :
- 825 est divisible par 11 ; (825 = 11 x 75); alors que 8 + 5 ≠ 2.
Critère de divisibilité par 14
Un nombre est divisible par 14 s’il est à la fois divisible par 7 et par 2.
Critère de divisibilité par 13
Lemme de divisibilité par 13
Le nombre
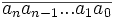
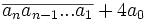
Exemples
637 est divisible par 13 car
- 63 + 4 x 7 = 91
- et 91 est divisible par 13.
D'une manière plus générale il suffit de répéter l'opération ci-dessus jusqu'à obtenir comme résultat final 13, 26 ou 39. Ce qui prouvera que le nombre considéré au départ est divisible par 13.
Soit le nombre 224185. On a :
- 22418 + 4 × 5 = 22438
- 2243 + 4 × 8 = 2275
- 227 + 4 × 5 = 247
- 24 + 4 × 7 = 52
- 5 + 4 × 2 = 13
Nous obtenons 13 donc 224185 est divisible par 13.
Critère pour un grand nombre
Supposons que l'on veuille savoir si un nombre contenant un grand nombre de chiffres est divisible par 13.
Il suffit de séparer ce nombre par tranche de 3 chiffres en partant des unités et d'insérer alternativement des - et des + entre les tranches à partir du début du nombre en commençant par un -.
On effectue l'opération ainsi écrite et si le résultat est divisible par 13, alors le grand nombre considéré est divisible par 13.
Bien sûr pour voir si le résultat de l'opération précédente est divisible par 13, on peut utiliser le lemme de divisibilité par 13.
Exemple
Soit le nombre 1633123612311854.
On le sépare par tranche de trois à partir des unités.
- 1 | 633 | 123 | 612 | 311 | 854.
On intercale alternativement des + et des - à partir du début en commençant par un -.
- 1 - 633 + 123 - 612 + 311 - 854.
On effectue l'opération ainsi écrite.
- 1 - 633 + 123 - 612 + 311 - 854 = -1664
Le résultat est négatif, mais on peut prendre sa valeur absolue 1664 et continuer.
On regarde si 1664 est divisible par 13 à l'aide du lemme de divisibilité par 13.
- 166 + 4×4 = 182
- 18 + 4×2 = 26
26 est divisible par 13 donc 1633123612311854 est divisible par 13.

















































