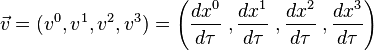Ligne d'univers - Définition

Les lignes d'univers comme outils pour décrire des évènements

Une ligne d'univers, une feuille d'univers et un volume d'univers, engendrés par une particule ponctuelle, une corde, et une brane.

Une ligne ou courbe unidimensionnelle peut être représentée par les coordonnées comme une fonction d'un paramètre. Chaque valeur a un point dans l'espace-temps et, variant le paramètre, il trace une ligne. Donc, en termes mathématiques, une courbe est définie par quatre fonctions coordonnées (quand dénote un temps coordonné) qui dépend d'un paramètre . Une grille coordonnée dans l'espace-temps est un ensemble de courbes que l'on obtient si trois des quatre fonctions sont des constantes.

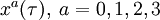
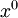
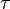
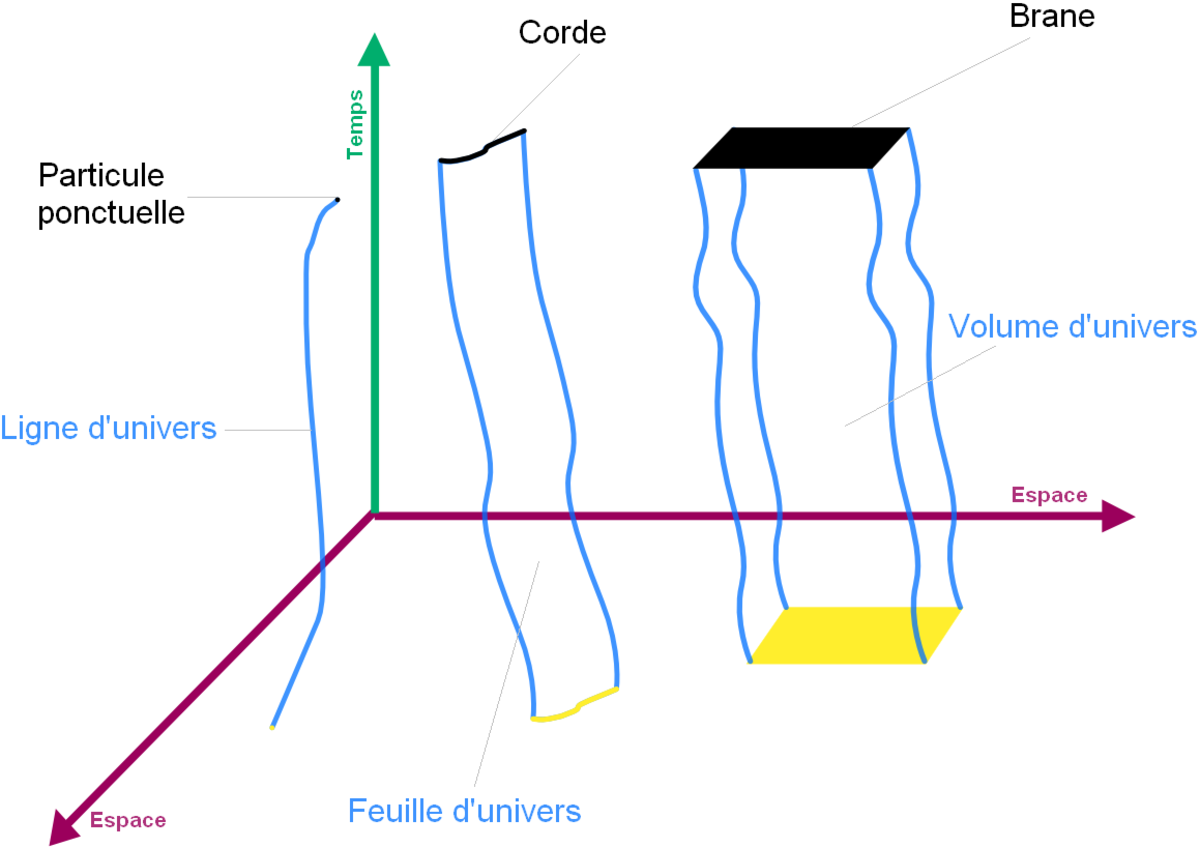
Quelquefois, le terme « ligne d'univers » est librement utilisé pour n'importe quelle courbe d'espace-temps. Cette terminologie pose problème. Plus convenablement, une ligne d'univers est une courbe dans l'espace-temps qui trace l'histoire (le temps) d'une particule, d'un observateur, ou plus généralement, d'un objet. On prend généralement le temps propre d'un objet ou d'un observateur comme paramètre de la courbe le long de la ligne de temps.

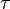
Exemples triviaux de courbes d'espace-temps

Différentes lignes d'univers voyageant à différentes vitesses constantes.
t représente le temps et x représente la distance.

Une courbe qui consiste en un segment de ligne horizontale (une ligne au temps coordonné constant) peut représenter une tige dans l'espace-temps et ne serait pas une ligne d'univers dans le sens propre du terme. Le paramètre trace la longueur de la tige.

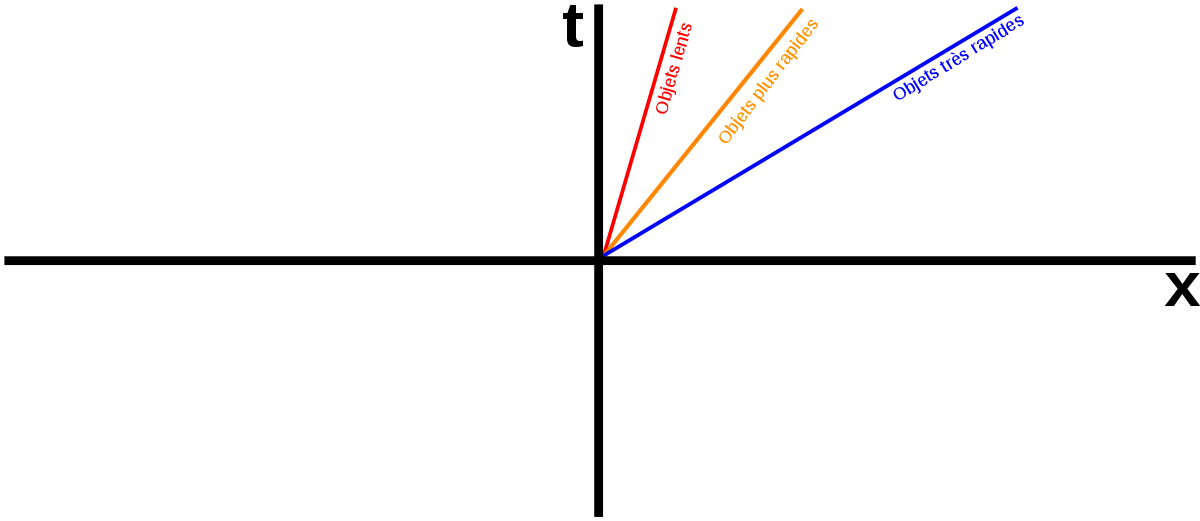
Une ligne à espace coordonné constant (une ligne verticale, par convention) peut représenter une particule au repos (ou un observateur stationnaire). Plus la ligne se rapproche de l'horizontale, plus grande est la vitesse.

Deux lignes d'univers qui démarrent séparément et qui s'entrecoupent par la suite signifient une collision ou une rencontre. Deux lignes démarrant au même événement dans l'espace-temps, chacune suivant par la suite son propre chemin, peuvent représenter la décadence d'une particule dans deux autres émissions ou une émission d'une particule par une autre.

Les lignes d'univers d'une particule et d'un observateur peuvent être interconnectées avec la ligne d'univers d'un photon et former un diagramme qui décrit les émissions d'un photon par une particule qui sera ensuite observée par l'observateur (ou absorbée par une autre particule).

Vecteur tangent à une ligne d'univers, de dimension quatre

Les quatre fonctions coordonnées définissant une ligne d'univers, sont les fonctions réelles d'un vrai variable, et peuvent simplement être différentiées dans les calculs usuels. Sans l'existence d'une métrique, on ne peut parler de la différence entre un point sur la courbe au paramètre de la valeur et un point sur la courbe (paramètre ) situé un peu plus loin. Dans la limite , cette différence divisée par défini un vecteur, le vecteur tangent de la ligne d'univers au point . C'est un vecteur de dimension quatre, défini dans le point . Il est associé avec la vélocité normale tridimensionnelle d'un objet (mais ce n'est pas le même) et donc appelé de vélocité quatre, ou dans les composants :

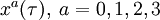
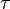
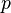
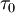
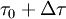
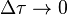
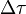
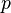
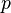
où les dérivées sont prises en compte au point , ainsi, τ = τ₀.

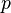
Toutes les autres courbes passant à travers le point ont un vecteur tangent, et pas seulement des lignes d'univers. La somme de deux vecteurs est encore un vecteur tangent pour certaines autres courbes et la même base pour multiplier par un scalaire. Par conséquent, tous les vecteurs tangents en un point traversent un espace linéaire, appelé espace tangent au point . Par exemple, prenons un espace bidimensionnel, comme la surface courbe de la Terre, son espace tangent à un point spécifique serait l'approximation plane de l'espace courbé.

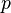
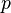
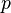
Imaginons un pendule flottant dans l'espace. Nous imaginons dans notre tête quatre étapes dans le temps : « Maintenant », « Puis », « Avant », et le « Passé ». Imaginons le pendule se balançant ainsi que le tic-tac du mécanisme interne. Chaque balancement de droite à gauche représente un mouvement dans l'espace, et la période entre un tic et un tac représente une période de temps.

Maintenant, visualisons une ligne ondoyante entre les différentes situations du pendule aux intervalles de temps : « Maintenant », « Puis », « Avant », et le « Passé ». La ligne est une ligne d'univers et est une représentation de la position du pendule dans l'espace-temps à n'importe quel point entre les intervalles. Le temps s'écoule donc entre « Passé » et « Maintenant ».