Lexique de la théorie des graphes - Définition

F

• Facteur : un k-facteur est un sous-graphe couvrant k-régulier.
• Feuille (dans un arbre) : sommet de degré 1.
• Fini (graphe) : un graphe est dit fini si le nombre de ses arêtes et de ses sommets est fini. Un graphe infini dont chaque sommet a un degré fini est dit localement fini.
• Forêt : graphe non-orienté acyclique. Chaque composante connexe d'une forêt forme un arbre.

I

• Incidence (matrice) : La matrice d'incidence d'un graphe G = (V,E) est la matrice de dimensions | V | x | E | dans laquelle l'entrée b_ij vaut 1 si le sommet v_i est une extrémité de l'arête x_j, 2 si x_j est une boucle sur v_i et 0 sinon. Dans le cas orienté, on a b_ij = − 1 si x_j sort de v_i et 1 si elle y rentre.
• Indépendant : deux sommets sont indépendants s'ils ne sont pas connectés, c'est-à-dire pas adjacents. Un ensemble de sommets est indépendant (ou stable) s'il n'y a pas deux de ses sommets adjacents.
• Infini : contraire de fini.
• Intervalle : un graphe d'intervalle est un graphe G tel que l'on puisse associer à chacun de ses sommet un intervalle sur l'ensemble des réels et tel que pour chaque sommet u et v de G il y a une arête entre u et v si et seulement si l'intersection entre leurs intervalles associés n'est pas nulle,
• Invariant : Propriété du graphe dépendant uniquement de sa structure (i.e. indépendante de son étiquetage). Par exemple, le degré moyen du graphe ou son spectre.
• Isolé : sommet de degré 0, c'est-à-dire n'ayant pas de voisin.
• Isomorphisme : un isomorphisme de graphe est un morphisme de graphe bijectif (ou inversible).
• Isomorphe : deux graphes sont isomorphes s'il existe un isomorphisme de graphe de l'un vers l'autre. C'est-à-dire s'ils ont exactement la même structure. Il suffit de remplacer les étiquettes des sommets pour qu'un graphe soit la copie conforme de l'autre.
• Isospectral : voir cospectral.

H

• Hamiltonien : un graphe est hamiltonien s'il a au moins un cycle passant par tous les sommets exactement une fois, et ce cycle est appelé cycle hamiltonien. Un cycle hamiltonien est aussi un cycle élémentaire de même ordre que le graphe.
• Hypergraphe : généralise la notion de graphe en autorisant une arête à relier plus de deux sommets.

J

• Jumeau : deux sommets sont jumeaux s'ils ont le même voisinage. Des vrais jumeaux respectent en plus la contrainte d'être voisins l'un de l'autre, et si cette contrainte n'est pas respectée alors on parle de faux jumeaux. La notion de voisinage peut-être généralisée pour une distance supérieure à 1 : on défini le voisinage de jusqu'à distance r par , et deux jumeaux ont alors .

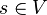
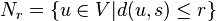
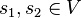
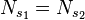
M

• Maille (ou girth en anglais) : longueur du plus court cycle. Si un graphe est acyclique, sa maille est considérée comme infinie. La maille paire (respectivement maille impaire) est la longueur du plus court cycle de longueur paire (respectivement impaire).
• Mineur : un graphe H est un mineur de G s'il est isomorphe à un graphe pouvant être obtenu en contractant zéro ou plus arêtes de G.
• Morphisme : application entre deux graphes qui respecte la structure de ces graphes.
• Multigraphe : un graphe doté d'une ou plusieurs arêtes multiples.

L

• Laplacienne (matrice) : matrice L = D − A où D est la matrice des degrés et A la matrice d'adjacence; on obtient sa forme normalisée L' par L' = D ^{− 1 / 2}LD ^{− 1 / 2} = I − D ^{− 1 / 2}AD ^{− 1 / 2}, où I dénote la matrice identité. Est utilisée dans la théorie spectrale des graphes.
• Libre d'échelle : un graphe est libre d'échelle si la distribution de ses degrés est proche d'une loi de puissance. Cette notion provient de la physique, et les divergences locales ou l'écart de la distribution par rapport à une loi de puissance ne sont pas spécifiés.
• Line graph : le line graph d'un graphe G est le graphe L(G) où on inverse sommets et arêtes, c'est-à-dire que deux sommets adjacents dans le line graph correspondent à deux arêtes incidentes à un même sommet dans G.