Lexique de la théorie des graphes - Définition

B

• Biparti : un graphe est dit biparti s'il existe une partition de son ensemble de sommets en deux sous-ensembles U et V telle que deux sommets adjacents soient dans deux parties différentes. Cela revient à dire que le graphe est 2-coloriable.
• Biparti complet : un graphe est dit biparti complet s'il est biparti et qu'il existe une arête entre chaque sommet de U et de V. On note K_m,n le graphe biparti complet tel que | U | = m et | V | = n.
• Boucle : arête partant d'un sommet et arrivant sur lui-même.

E

• Espace : soit un graphe G = (V,E). L'espace des sommets est l'espace vectoriel sur {0,1} avec comme base {v₁,...,v_n}, soit un espace de dimension n. De même, l'espace des arêtes est l'espace vectoriel sur {0,1} avec comme base {e₁,...,e_m}, soit un espace de dimension m. Le principe du 0 est du 1 est qu'on obtient 1 pour un sommet (ou arête) appartenant à l'espace et 0 sinon.
• Étiquetage : fonction associant chaque sommet à une étiquette, pouvant être dans n'importe quel ensemble (réels, mots, couleurs...).
• Eulérien : un chemin eulérien est un chemin qui passe par toutes les arêtes exactement une fois. Un cycle eulérien est un chemin eulérien où les sommets de départ et d'arrivés sont les mêmes. Un graphe où l'on peut construire un cycle eulérien est appelé graphe eulérien; si l'on ne peut construire que des chemins eulériens, alors le graphe est semi-eulérien. Un graphe est eulérien si chaque sommet est de degré pair.
• Excentricité : l'excentricité d'un sommet est sa distance maximale à tous les autres sommets.
• Expansion : si H est un mineur de G (i.e. H résulte d'une série de contractions) alors G est une expansion de H. Une opération d'expansion remplace un sommet s par deux sommets s₁,s₂ connectés par une arête, et s₁ et s₂ sont connectés à tous les voisins de s. Dans le cas d'un plongement d'un graphe G₁ = (V₁,E₁) dans G₂ = (V₂,E₂), une expansion a une autre signification : il s'agit du rapport entre la taille des deux graphes, soit .
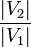
• Extra-planaire : voir outer-planar.

D

• Degré : dans le cas non-orienté, le degré d(s) du sommet s est le nombre d'arêtes de s. Dans le cas d'un graphe orienté, le degré entrant d ⁺ (s) est le nombre d'arcs vers s tandis que le degré sortant d ⁻ (s) est le nombre d'arcs sortant de s. Le degré maximum est noté Δ(G), et le degré minimal δ(G). Dans la matrice des degrés, l'entrée D_ii est le degré du sommet i.
• Diamètre : excentricité maximale des sommets, notée D.
• Dilatation : dans un plongement où f associe des sommets d'un graphe G à ceux d'un graphe H, la dilatation est la distance maximale entre les images par f de deux sommets adjacents dans G. Autrement dit, si deux sommets sont voisins dans un graphe, leurs images peuvent être séparées par un chemin qui augmente donc la distance entre eux, et la plus grande augmentation est la dilatation.
• Distance : la distance d_G(x,y) entre x et y est la longueur du plus court chemin entre ces sommets; aussi appelée distance géodésique.
• Distance (matrice de)  : matrice d'éléments a_ij correspondant a la longueur du plus court chemin (la distance) entre les sommets d'indices i et j.
• Distance-régulier : un graphe est distance-régulier si pour tous sommets , le nombre de sommets voisins de u à distance i et le nombre de sommets voisins de v à distance j ne dépendent que de i,j et de la distance d(u,v) entre u et v. Formellement, tels que c₀ = 0 et
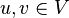
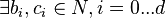
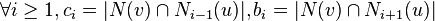
• Dominant (ou absorbant) : un ensemble de sommet est dominant si tout sommet en fait partie ou est voisin d'un sommet en faisant partie.