Lemme de Gauss (polynômes) - Définition

Introduction

En mathématiques il existe un résultat appelé lemme de Gauss s'appliquant à la théorie des polynômes. Il énonce que si un polynôme P à coefficients entiers est factorisé en deux polynômes à coefficients rationnels non constants, ceux-ci sont proportionnels à des polynômes à coefficients entiers dont le produit est égal à P.

Il existe une variante de ce lemme, stipulant un résultat analogue si l'anneau est factoriel. Il permet de démontrer le caractère factoriel de l'ensemble des polynômes à coefficients dans un anneau factoriel, précisant le type d'arithmétique des polynômes disponible pour ce cas particulier. Une démonstration du cas général est présenté dans l'article Anneau factoriel.

Ce lemme apparaît dans les Disquisitiones Arithmeticae de Gauss, à l'article 42, sous la forme d'une contraposée.

Énoncé

Démonstration

• Tout polynôme non nul à coefficients dans Q est produit d'un élément de Q et d'un polynôme à coefficients dans Z primitif :

Soit f un polynôme à coefficients dans Q. f est alors le produit d'une constante rationnelle et d'un polynôme à coefficients dans Z. En effet, soit π le produit des dénominateurs des différents coefficients de f. Soit g le polynôme défini par f = 1/π.g on remarque que g est bien un polynôme à coefficients dans Z.

Soit μ le plus grand commun diviseur des coefficients de g et h le polynôme défini par g = μ.h, on remarque que le polynôme h est primitif.

L'égalité f = μ/π.h permet de conclure.

• Il n'existe qu'une unique valeur strictement positive pour le contenu d'un polynôme f à coefficients dans Q non nul :

Supposons deux décompositions de f de la forme précédente :

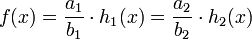
On en déduit l'égalité des deux polynômes à coefficients dans Z :

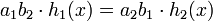
Un diviseur différent de +/-1 de a₁b₂ ne peut peut diviser chacun des membres de h₂ car sinon, le polynôme ne serait pas primitif. On en déduit que a₁b₂ divise a₂b₁. Un raisonnement analogue montre que a₂b₁ divise a₁b₂. Ces deux valeurs sont positives car les fractions a₁/b₁ et a₂/b₂ sont positives. Deux nombres strictement positifs qui ce divisent l'un l'autre sont égaux, ce qui démontre la proposition.

Dans la suite de la démonstration, le contenu est choisi toujours positif. Cette convention est toujours possible à remplir, quitte à multiplier le polynôme et le contenu par -1.

• Le produit de deux polynômes non nuls primitifs est primitif :

Soit h et h deux polynômes à coefficients non nuls primitifs, on les notes de la manière suivante :

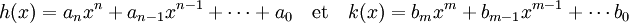
Soit p un nombre premier, montrons qu'il ne divise pas tous les coefficients du polynôme h.k. Il existe un entier i plus petit que n tel que a_i ne soit pas multiple de p, sinon tous les coefficients de h seraient multiple de p et h ne serait pas primitif. Soit μ le plus petit d'entre eux. De même soit ν le plus grand entier tel que b_ν ne soit pas un multiple de p. Calculons alors le coefficient du monôme de degré μ + ν de h.k, noté α_{μ + ν} :

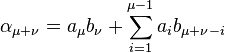
Remarque : il se peut que μ + ν - 1 soit plus grand que m, pour que la formule précédente soit valable, il faut utiliser la convention que b_j est égal à zéro si j est strictement plus grand que m.

L'expression trouvée de α_{μ + ν} comporte un terme qui n'est pas multiple de p et d'une somme de multiple de p, ce qui démontre que α_{μ + ν} n'est pas un multiple de p. Aucun nombre premier ne divise le contenu du produit car il existe toujours un coefficient non multiple de ce nombre premier. On en déduit ce contenu est égal à un, car par convention il est positif.

• Le contenu du produit de deux polynômes non nul à coefficients dans Q est égal au produit du contenu des deux polynômes :

Soit f et g deux polynômes, c et d leur contenu respectif et h et k les deux polynômes à coefficients dans Z et primitifs tel que f = c.h et g = d.k. L'égalité suivante montre que le contenu du produit est égal à c.d :

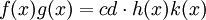
En effet, comme h et k sont deux polynômes non nuls primitifs leur produit est aussi primitif, ce qui termine la démonstration.

• Démonstration du lemme de Gauss :

Remarquons que le contenu d'un polynôme unitaire est plus petit que 1. En effet, soit P un polynôme unitaire, et c son contenu. On a alors P = c.Q, où Q est un polynôme à coefficients entiers primitif. En notant q le coefficient dominant de Q, on a 1 = cq, d'où c plus petit que 1. De plus, on voit que c = 1 si et seulement si P est à coefficients entiers.

Notons maintenant f et g les deux polynômes unitaires de l'énoncé. Les contenus sont donc tous deux inférieurs à 1, et l'un des deux est même strictement inférieur à 1, puisque l'un des polynômes n'est pas à coefficients entiers. Le contenu du produit f.g, qui est égal au produit des contenus, est donc strictement inférieur à 1, ce qui prouve que f.g n'est pas à coefficients entiers.