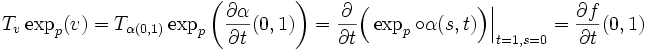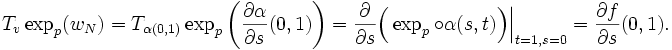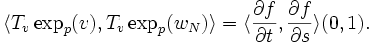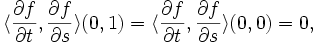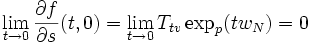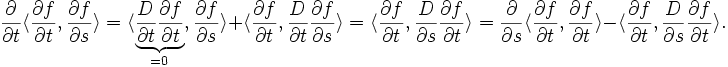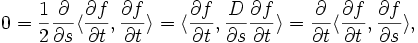Lemme de Gauss (géométrie riemannienne) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie riemannienne, le lemme de Gauss permet de comprendre l'application exponentielle comme une isométrie radiale. Dans ce qui suit, soit M une variété riemannienne dotée d'une connexion de Levi-Civita (i.e. en particulier, cette connexion est symétrique et compatible avec la métrique de M).
Introduction
Nous avons défini sur M l'application exponentielle en
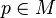
où on a dû restreindre le domaine TpM de définition à une boule Bε(0) de rayon ε > 0 et de centre 0 pour s'assurer que expp est bien définie et où γ(1,p,v) est le point
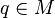
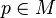
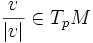
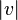
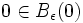
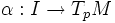
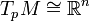
Le fait que expp soit un difféomorphisme local et que T0expp(v) = v pour tout
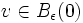
Ceci signifie en particulier qu'il est possible d'identifier la boule
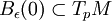
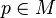
Ceci signifie en particulier qu'il est possible d'identifier la boule
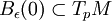
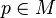
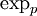
Lemme de Gauss : l'exponentielle comme isométrie radiale
Soit
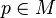
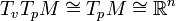
Soient
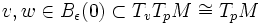
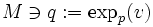
Pour
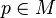
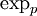
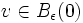
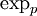
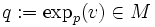
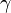
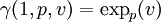
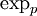
Preuve
Rappelons que
Nous procédons en trois étapes :
-
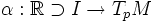
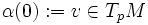
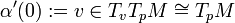
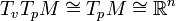
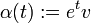
Calculons maintenant le produit scalaire
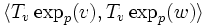
Décomposons
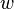
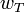
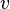
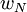
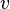
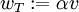
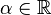
L'étape précédente implique alors directement :
Il faut donc montrer que le second terme est nul, car, selon le lemme de Gauss, on devrait avoir
-
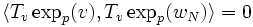
définissons la courbe
avec
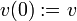
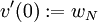
Posons alors
et calculons :
et
Donc,
On va vérifier maintenant que ce produit scalaire est en fait indépendant de la variable t, et donc que, par exemple,
car, selon ce qui a été donné plus haut,
étant donné que la différentielle est une application linéaire ! Ceci prouverait alors le lemme.
- On vérifie que
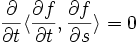
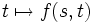
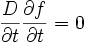
Donc, en particulier,
car on a | v | = cste.
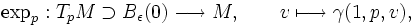
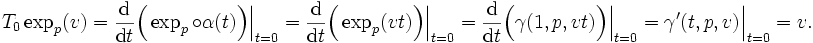
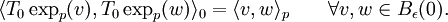
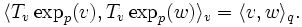
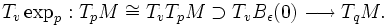
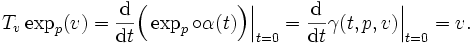
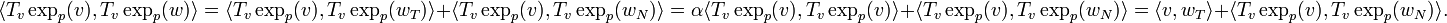
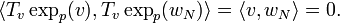
![\alpha : ]-\epsilon, \epsilon[\times [0,1] \longrightarrow T_pM,\qquad (s,t) \longmapsto t\cdot v(s),](https://static.techno-science.net/illustration/Definitions/autres/8/858acd50e9bf9b6c7d9a2a92e8470eed_d1ce0a5c9a2ecd186dce7cb4f54233e8.png)
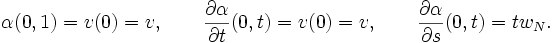
![f : ]-\epsilon, \epsilon[\times [0,1] \longrightarrow M,\qquad (s,t)\longmapsto \exp_p(t\cdot v(s)),](https://static.techno-science.net/illustration/Definitions/autres/f/f9d1593414a9807b10db2904f061dc83_d5cb62e72b39cebbe0986bd93e061078.png)