L-System - Définition

Introduction

Un L-System (ou système de Lindenmayer) est une grammaire formelle, permettant un procédé algorithmique, inventé en 1968 par le biologiste hongrois Aristid Lindenmayer qui consiste à modéliser le processus de développement et de prolifération de plantes ou de bactéries.

Basée sur une forme récursive de grammaire générative, cette grammaire a été approfondie et mise en œuvre graphiquement par Przemyslaw Prusinkiewicz dans les années 1980.

Au départ, Lindenmayer avait pensé ce système comme un langage formel qui permettait de décrire le développement d'organismes multicellulaires simples. À cette époque il travaillait sur les levures, les champignons et des algues. Mais l'informatique a permis d'exploiter ce système pour générer graphiquement des calculs de plantes très complexes.

Un L-System est un ensemble de règles et de symboles qui modélisent un processus de croissance d'êtres vivants comme des plantes ou des cellules. Le concept central des L-Systems est la notion de réécriture. La réécriture est une technique pour construire des objets complexes en remplaçant des parties d'un objet initial simple en utilisant des règles de réécriture.

Pour ce faire, les cellules sont modélisées à l'aide de symboles. À chaque génération, les cellules se divisent, i.e. un symbole est remplacé par un ou plusieurs autres symboles formant un mot.

Grammaire formelle

Un L-System est une grammaire formelle qui comprend :

1. Un alphabet V : l'ensemble des variables du L-System. V ^* est l'ensemble des "mots" que l'on peut construire avec les symboles de V, et V ⁺ l'ensemble des mots contenant au moins un symbole.
2. Un ensemble de valeur constantes S. Certains de ces symboles sont communs à tous les L-System (voir plus bas la ).
3. Un axiome de départ ω choisi parmi V ⁺ , c'est-à-dire l'état initial.
4. Un ensemble de règles, noté P, de reproduction des symboles de V.

Un L-System est alors noté {V,S,ω,P}.

Turtle interpretation

Cette chaîne de caractère est un mot insensé en soi, mais qui peut fort bien se prêter à une interprétation graphique, en deux ou trois dimensions. Pour illustrer la manière de construire une plante avec un L-System, imaginons que nous avons un crayon à la main et qu’elle se balade sur la feuille sous nos ordres : "monte d’un cran, puis tourne de 20° à gauche, déplace toi deux fois de un cran, mémorise ta position et avance encore d’un cran, lève-toi puis repose-toi sur la position mémorisée" et ainsi de suite... Il a donc fallu inventer des symboles variants ∈ V, ou constants ∈ S, pour permettre de guider cette main. Plusieurs d'entre eux ont été normalisés, ils font partie de ce qu'on appelle la "Turtle interpretation". Ce nom vient de la "tortue" du langage de programmation Logo qui fonctionne sur le même principe. En fait c'est cette tortue qui est votre main qui tient le crayon. Voici donc les signes couramment utilisés :

• F : Se déplacer d’un pas unitaire (∈ V)
• + : Tourner à gauche d’angle α (∈ S)
• - : Tourner à droite d’un angle α (∈ S)
• & : Pivoter vers le bas d’un angle α (∈ S)
• ^ : Pivoter vers le haut d’un angle α (∈ S)
• < : Roulez vers la gauche d’un angle α (∈ S)
• > : Roulez vers la droite d’un angle α (∈ S)
• | : Tourner sur soi-même de 180 ° (∈ S)
• [ : Sauvegarder la position courante (∈ S)
• ] : Restaurer la dernière position sauvée (∈ S)

Pour être plus concret, les symboles appartenant à V sont des parties d'une plante, comme une branche ou une portion de branche tout simplement. Les symboles appartenant à S sont des ordres que l'on donne à notre main virtuelle qui dessine la plante, ils servent à déterminer une direction à prendre, tandis que les symboles de V dessinent dans cette direction.

Remarque : Les deux derniers symboles rappellent les fonctions pushMatrix() et popMatrix() d'OpenGl, ainsi on devine que c'est un environnement graphique qui se prêtera très bien au L-System. De plus la programmation orientée objet avec les pointeurs, tel que dans le langage C++, semble indiquée pour la modélisation d'une "chaîne cellulaire" qui évolue.

Exemple de la courbe de Koch

• Variable : v = {F}
• Constantes : S = {+, −}
• Axiome : w = F
• Règle : (F → F+F−F−F+F)

Courbe_de_Koch
{
angle 90
axiom F
F=+F−F−F+F
}

angle 90 détermine que l'on tourne de 90 ° avec les symboles + et -.

Voici le résultat sur trois générations :

• n=0:

F

• n=1:

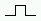
F+F-F-F+F

• n=2:

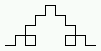
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

• n=3:

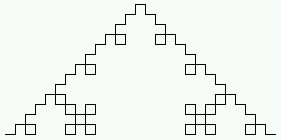
F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+ F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F- F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F+ F+F-F-F+F+F+F-F-F+F-F+F-F-F+F-F+F-F-F+F+F+F-F-F+F

Turtle en trois dimensions

Cette « turtle interpretation » peut être exploitée en trois dimensions grâce aux idées de Harold Abeson et Andrea diSessa dans leur ouvrage commun, « Turtle geometry : the computer as a medium for exploring mathematic ». L'orientation est représentée par trois vecteurs :
, , tels que

• pour turtle heading. Il s'agit du regard de la tortue.
• pour up. Il s'agit de la direction vers laquelle se dirige la tortue.
• pour left. Il s'agit de la gauche de cette tortue.

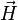
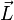
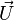
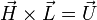
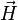
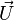
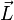
La rotation de la tortue se note alors :
Où R est une matrice 3×3. Les rotations d'un angle α autour des axes , ou sont représentées par les matrices :

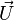
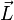
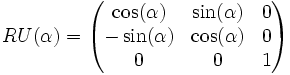
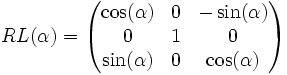
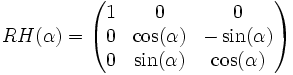
Les symboles prennent maintenant la signification suivante :

• + Tourner à gauche d'un angle α, en utilisant la matrice de rotation RU(α).
• − Tourner à droite d'un angle α, en utilisant la matrice de rotation RU(−α).
• & Pivoter vers le bas d'un angle α, en utilisant la matrice de rotation RL(α).
• ∧ Pivoter vers le haut d'un angle α, en utilisant la matrice de rotation RL(−α).
• \ Rouler à droite d'un angle α, en utilisant la matrice de rotation RH(α).
• / Rouler à gauche d'un angle α, en utilisant la matrice de rotation RH(−α).
• | Tourner autour de lui-même de 180 °, en utilisant la matrice de rotation RU(180◦).