Johannes Kepler - Définition

Kepler et l’astrologie

Kepler était persuadé que l’astrologie pouvait devenir une science au même titre que la physique ou les mathématiques. Il était convaincu que les positions des planètes affectaient les humains et influençaient la météorologie terrestre. Pour lui, astronomie et astrologie étaient liées. C’est ainsi qu’il essaya de poser des bases scientifiques rigoureuses à l’astrologie en faisant intervenir les principes physiques de son époque, essentiellement autour de considérations sur la nature de la lumière. Par exemple différences entre lumière propre (du soleil) et lumière réfléchie (de la lune, mais aussi des planètes), etc.

La publication de ses horoscopes et de ses prédictions lui fit une bonne renommée. En 1595, il prédit un soulèvement de la population, une invasion turque ainsi qu’un hiver rigoureux. Il se trouve que de tels événements se produisirent. Il compila plus tard l’horoscope du général Albrecht von Wallenstein qui s’arrêta par un « violent événement » en 1634. Wallenstein fut en effet assassiné le 24 février de cette année. Il laissa trois écrits sur l’astrologie : De fundamentis astrologiae, en 1601 ; le Tertius interveniens en 1610 et Astrologicus, en 1620.

Il attribue d’ailleurs aux astres le malheur et le comportement de ses parents, qu’il croit nés sous une mauvaise étoile, ainsi que son premier mariage — décevant — sous un « ciel calamiteux ».

Il est par ailleurs très critique vis à vis de l'astrologie populaire et de ses prédictions, comme de tout temps (aujourd'hui encore) les astrologues « savants » ont critiqué les astrologues « populaires » sans réussir à définir la ligne de démarcation. Le De fundamentis astrologiae de 1601 par exemple, est un mini-traité visant à fonder physiquement l'astrologie (contre la tradition, ce pourquoi le Tertius interveniens 1610 est une réponse aux objections formulées par quelques astrologues de son temps contre ses considérations « physiques » sur l'astrologie). Kepler préconisa de ne conserver de l'astrologie que les aspects et de ne pas considérer les positions zodiacales. Il ne fut guère suivi dans cette direction si ce n'est en augmentant le nombre des aspects (comme le quintile de 72°) Il y établit quelques prédictions (essentiellement météorologiques) pour l'année 1602 suite à la mort, quelques semaines plus tôt, de Tycho Brahe, « Le Phénix des astronomes » (thèse 6). Dans l'introduction de ce texte, Kepler explique qu'il va s'atteler à cette tâche « puisqu'il le faut ». C'est en effet l'une des responsabilités liées à la fonction d'astronome impérial dont il a hérité avec le décès inattendu de Tycho Brahe.

Œuvres scientifiques

Kepler a découvert les relations mathématiques (dites lois de Kepler) qui régissent les mouvements des planètes sur leur orbite. Ces relations sont fondamentales car elles furent plus tard exploitées par Isaac Newton pour élaborer la théorie de la gravitation universelle. Toutefois, bien qu'il ait vu juste quant à la forme des orbites planétaires, Kepler expliquait les mouvements des planètes par le magnétisme, l'idée d'une attraction entre les masses n'existant pas encore.

Il a enfin accordé une attention majeure à l’optique en synthétisant en 1604, puis en 1611, les principes fondamentaux de l’optique moderne comme la nature de la lumière, la chambre obscure, les miroirs (plans et courbes), les lentilles ou la réfraction.

Le Mysterium Cosmographicum

En 1596, il publie son premier ouvrage, Mysterium Cosmographicum, fruit de ses premières recherches sur la structure de l’Univers. Il voit dans les lois qui régissent les mouvements des planètes un message divin adressé à l’Homme. Dans ce livre, où il affirme sa position copernicienne, il se donne pour objectif de répondre à trois questions portant sur le nombre de planètes, leur distance au Soleil et enfin leur vitesse.

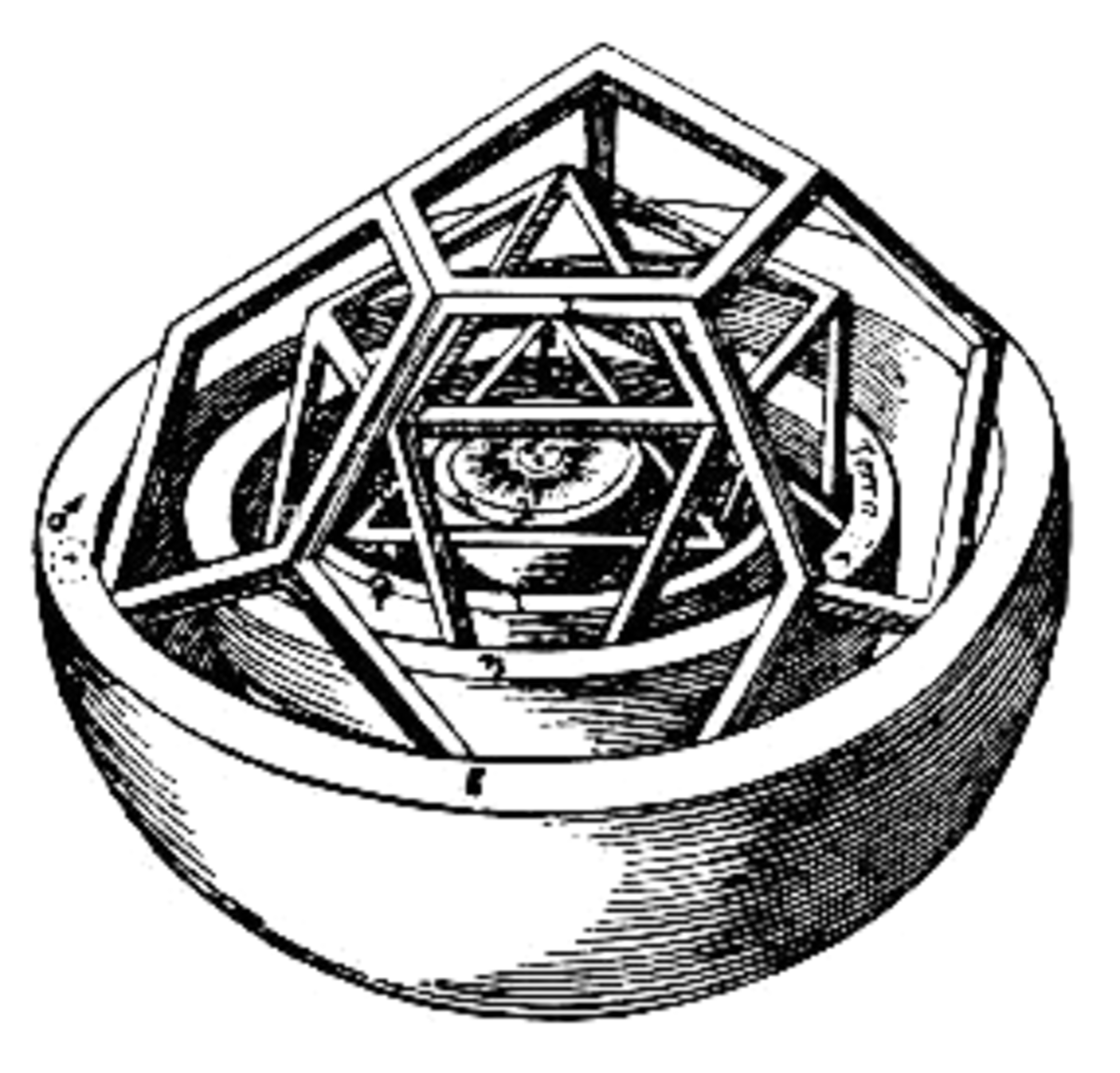
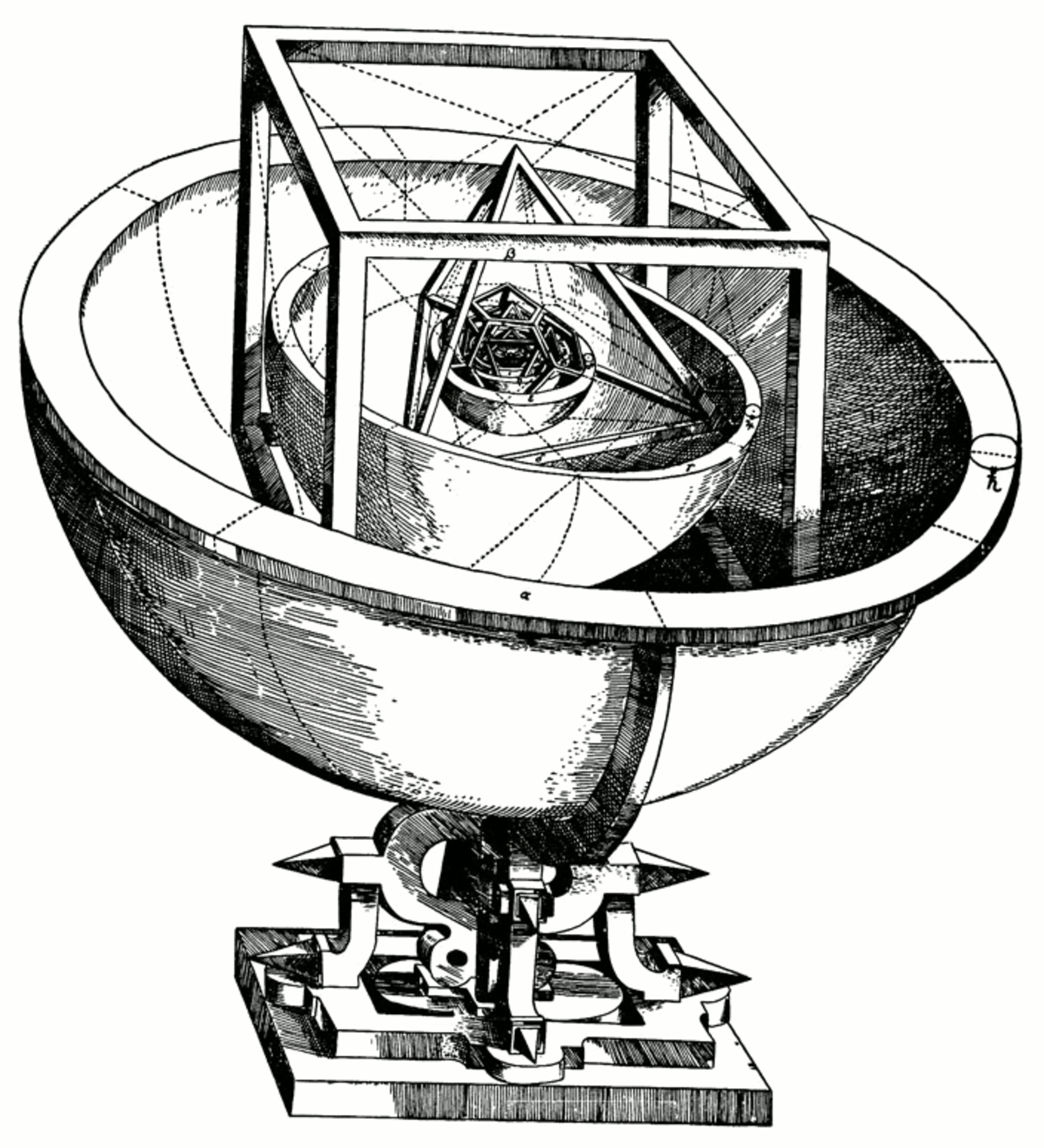
Dans son livre, il développe une théorie des polyèdres réguliers permettant de construire un modèle de l’Univers. Kepler remarqua que l'on pouvait intercaler entre les orbes des six planètes connues à l’époque (de Mercure à Saturne) les cinq solides de Platon. Ces derniers étant des polyèdres réguliers, ils étaient parmi les solides ceux qui approchaient le plus la perfection divine de la sphère. Leur utilisation dans l'architecture de l'Univers s'accordait bien avec la grandeur de la création divine. Le nombre de ces solides impliquait le nombre de planètes : cinq intervalles, donc six planètes.

Mais ces polyèdres expliquaient également, par leur disposition, les proportions des orbes planétaires (les distances relatives des planètes au Soleil) : chaque solide était inscrit dans l'orbe d'une planète et circonscrit à l'orbe de la planète immédiatement inférieure. L'emboîtement était constitué ainsi : le cube entre les orbes de Saturne et de Jupiter, le tétraèdre entre celui de Jupiter et celui de Mars, puis le dodécaèdre, entre ce dernier et celui de la Terre, suivi par l'icosaèdre englobant l'orbe de Vénus, lui-même circonscrit à l'octaèdre, qui entourait enfin l'orbe de Mercure.
Pour prendre en compte la variabilité de la distance des planètes au Soleil (due pour Kepler comme pour Copernic à l'excentricité et aux épicycles de chacune d'entre elles), l'astronome donne à chaque orbe une épaisseur correspondant à la différence entre la distance maximale et la distance minimale de la planète au Soleil. Il est à noter que l'épaisseur des orbes amène Kepler à transformer de façon décisive le système copernicien en un système réellement héliocentrique : en effet, Copernic prenait comme référence des mouvements planétaires le centre du grand orbe (l'orbe terrestre), et non le Soleil, un peu à l'écart du fait de l'excentricité de l'orbite terrestre. Pour affecter à l'orbe de la Terre, comme à toutes les autres, une épaisseur, Kepler déplace la référence des mouvements planétaires dans le Soleil.

Reste la question des vitesses. Pour les expliquer, il attribue au Soleil une «âme» ou «force» motrice qui induit le mouvement des planètes. Il compare celle-ci avec la lumière, qui elle aussi provient du Soleil, et tente de déduire de cette analogie une loi mathématique liant la période de révolution des planètes à leur distance moyenne au Soleil. Mais ses conceptions erronées sur la propagation de la lumière (qu'il corrigera par la suite), sur la dynamique (relations entre forces et mouvements, qui seront établies par Galilée et Newton), ainsi que des erreurs sur les déductions mathématiques des principes qu'il établit, l'amènent à une loi erronée, qu'il lui faudra plus de vingt ans pour rectifier (dans l').

La théorie des solides emboîtés, qui amènera plus tard Kepler à découvrir deux nouveaux solides réguliers (voir Les polyèdres de Kepler-Poinsot), si elle nous paraît fantaisiste aujourd’hui, a permis à Kepler d’entrer en contact avec ses contemporains Galilée et Tycho Brahe, mathématicien impérial à la cour de Prague. Le premier lui fit part de son enthousiasme pour le soutien des idées coperniciennes qu’il partage également. Le second, tout aussi admiratif, l’invita à travailler à ses côtés.

Mais les apports du Mysterium Cosmographicum ne se limitent pas à la riche collaboration qu'il a permise avec l'astronome danois. Ce livre a surtout été apprécié en son temps car il constituait le premier plaidoyer convaincant pour la théorie copernicienne, ne se contentant pas, ainsi que Rheticus l'avait fait, de présenter les avantages du système héliocentrique du point de vue mathématique. Kepler, en effet, cherche (et croit avoir trouvé) les causes (physiques et métaphysiques) du nombre, de la disposition et des mouvements des planètes. Cette recherche des causes (physiques), que Kepler poursuivra tout au long de sa vie, constitue l'acte fondateur de l'invention d'une nouvelle science : l'astrophysique.

Le calcul de l’orbite de Mars

Poursuivi pour ses convictions religieuses et ses idées coperniciennes, Johannes Kepler doit quitter Graz en 1600. Il se réfugie à Prague, invité par l’astronome danois Tycho Brahe pour y devenir son assistant. Les relations entre les deux personnages furent particulièrement houleuses ; Tycho Brahe ne croyant pas à l’héliocentrisme de Copernic mais soutenant une autre théorie dans laquelle la Terre est au centre mais les autres planètes tournent autour du Soleil.

Kepler voyait en Tycho Brahe un homme plein de richesses (ses mesures étaient les plus précises jamais réalisées) mais qui ne savait les exploiter correctement.

Brahe lui demanda de calculer l’orbite précise de Mars, dont les positions suivant ses observations résistaient à toute tentative de modélisation, et s'écartaient notablement (de plusieurs degrés) de celles prévues par les tables. Cette tâche était auparavant assignée à son assistant Longomontanus qui passe alors à l’étude des mouvements de la Lune.

Pensant accomplir sa tâche en quelques semaines, il ne lui fallut pas moins de six ans pour achever son travail. C’est durant ce travail que Johannes Kepler découvrit les deux premières des trois lois fondamentales :

• Les planètes décrivent des trajectoires elliptiques dont le Soleil est un foyer.
• Le mouvement de chaque planète est tel que le segment de droite reliant le Soleil et la planète balaie des aires égales pendant des durées égales.

Ces lois furent publiées dans Astronomia Nova en 1609, où Johannes Kepler fut également le premier à émettre l’hypothèse d’une rotation du Soleil sur son axe.

En 1618 viendra sa troisième grande loi :

• Pour toutes les planètes, le rapport entre le cube du demi grand axe de la trajectoire et le carré de la période est le même — cette constante est indépendante de la masse de la planète.

Ce travail fut d’autant plus long que Kepler dut mener en parallèle une étude sur l’optique afin de mieux comprendre et interpréter ses observations, et qu’il était encore trop « conditionné » par les anciennes croyances en astronomie : il doute à plusieurs reprises de la nature circulaire de la trajectoire et pense alors à une ellipse, tout en continuant d’essayer de prouver le contraire, en ressortant de vieilles idées faisant appel à l’utilisation d’épicycles.

Les soixante-dix chapitres de l’Astronomia Nova comprennent ainsi toutes les démarches scientifiques et erreurs de Kepler qui lui permirent d’aboutir à ses deux premières lois, mais aussi à d’autres conclusions intéressantes comme la nature de la force responsable du mouvement des planètes, force « quasi magnétique », donc physique et non plus divine.

À la mort de Tycho Brahe en 1601, Johannes Kepler fut désigné comme mathématicien impérial à la cour de Rodolphe II. Il garda ce statut jusqu’en 1612.

L’optique

Alors qu’il étudie l’orbite de Mars, Kepler voit la nécessité d’étudier également l’optique afin de mieux comprendre certains phénomènes observés tels la réfraction atmosphérique. Dès 1603, il parcourt divers ouvrages sur le sujet dont celui de l’Arabe Alhazen.

Kepler rassemble les connaissances de l’époque dans son livre Astronomia pars Optica, publié en 1604. Il y explique les principes fondamentaux de l’optique moderne comme la nature de la lumière (rayons, intensité variant avec la surface, vitesse infinie, etc.), la chambre obscure, les miroirs (plans et courbes), les lentilles et la réfraction dont il donne la loi i = n×r, qui est correcte pour de petits angles (la vraie loi — sin i = n×sin r — fut donnée plus tard par Willebrord Snell et René Descartes). Il aborde également le sujet de la vision et la perception des images par l’œil. Il est convaincu que la réception des images est assurée par la rétine et non pas le cristallin comme on le pensait à cette époque, et que le cerveau serait tout à fait capable de remettre à l’endroit l’image inversée qu’il reçoit.

En 1610, il prend connaissance de la découverte de quatre satellites autour de Jupiter grâce aux observations de Galilée avec sa lunette astronomique et écrit une lettre de soutien publiée sous le titre de Dissertatio cum Nuncio Sidero (Conversation avec le messager des étoiles), puis après avoir lui-même observé ces satellites, il publie ses observations dans Narratio de Observatis Quatuor Jovis Satellibus. C’est d’ailleurs Kepler qui, le premier, dans son ouvrage de 1611, utilisa le mot « satellite » pour désigner les quatre petits astres tournant autour de Jupiter.

L’invention récente de la lunette enthousiasme beaucoup Kepler qui, en 1611, écrit un second ouvrage d’optique, Dioptricae, reprenant de nombreux thèmes abordés dans l’Optica en les approfondissant. Dans ce livre très mathématique, il rassemble 141 théorèmes visant à faire la théorie des lentilles et de leurs associations possibles, dont la théorie de la lunette de Galilée que ce dernier n'avait pas faite.

L’Harmonie du monde

Kepler crut découvrir grâce à des travaux antérieurs que l’Univers était soumis à des lois « harmoniques », faisant un lien entre l’astronomie et la musique. Dans le Harmonice Mundi, publié en 1619, il attribue aux planètes un thème musical. Les variations des vitesses de ces planètes sont représentées par les différentes notes composant la musique. Ainsi, il était facile de distinguer les orbites les plus excentriques. Mais c’est aussi dans cet ouvrage en cinq volumes que Kepler énonce sa troisième loi fondamentale : « le carré de la période est proportionnel au cube du demi-grand axe [de l'ellipse] ». Celle-ci découle de ses recherches sur un modèle d’Univers harmonique.

Ses autres travaux

Suite à l’observation d’une supernova en 1604-1605, il écrira deux ans plus tard De Stella nova in pede serpentarii.

L’année 1613 est marquée par la publication d’un travail sur la chronologie et l’année de naissance de Jésus de Nazareth. D’abord en allemand, puis en latin l’année suivante (De Vero Anno quo Aeternus Dei Filius Humanam Naturam in Utero Benedictae Virginis Mariae Assumpsit). Il y démontra que le calendrier chrétien comportait une erreur de cinq ans et fut ainsi le premier à revoir la date de naissance de Jésus, en l’an -4.

Entre 1617 et 1621, il écrit Epitome Astronomiae Copernicae, une introduction à l’astronomie copernicienne.

Il construisit une table de logarithmes, publiée en 1624 dans Chilias logarithmorum à Marbourg, en améliorant la méthode de calcul proposée par John Napier. Bien qu’achevées depuis un moment déjà, il publia à Ulm, en 1627, ses tables rudolphines (Tabulae Rudolphinae) en hommage à Rodolphe II. Ces tables de positions planétaires étaient fondées sur les observations de Tycho Brahe et de ses propres travaux sur la mécanique céleste. Ce retard était dû à un différend avec les héritiers de Tycho Brahe qui ne voulaient pas que les travaux de Tycho soient exploités sans percevoir une partie des gains, ainsi qu’à leur demande de modification de l’introduction de l’ouvrage. Lors de son séjour à Ulm, il est chargé, avec Faulhaber, de définir des unités de mesure pour les activités commerciales et militaires.

Il émit la conjecture mathématique appelée « conjecture de Kepler » concernant l’empilement des sphères (ou des boulets de canons). Celle-ci n’a été démontrée par l’Américain Thomas C. Hales qu’en 2003 et encore pas tout à fait suivant les critères des mathématiciens. Elle énonce que, dans l’espace, l’empilement des sphères le plus dense est celui du marchand des quatre saisons à savoir le cubique face centrée (voir système cristallin).