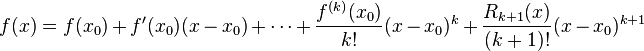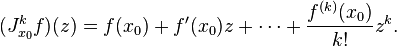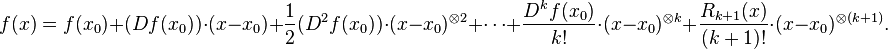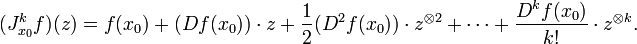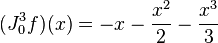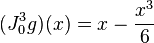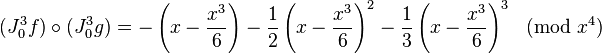Jet (mathématiques) - Définition

Introduction

En mathématiques, un jet est une opération qui, en chaque point de son domaine, associe à une fonction différentiable f un polynôme : la série de Taylor de f tronquée. Bien que ceci soit la définition d'un jet, la théorie des jets considère ces polynômes comme des polynômes formels plutôt que des fonctions polynomiales.

Cet article explore d'abord la notion de jet d'une fonction d'une variable réelle à valeur réelle, suivie d'une discussion de la généralisation à plusieurs variables. Ensuite, il donne une construction rigoureuse des jets et des espaces de jets entre espaces euclidiens. Il conclut par une description des jets entre variétés, et d'une construction intrinsèque de ces jets. Dans ce cadre plus général, il donne un résumé de quelques unes des applications des jets à la géométrie différentielle et à la théorie des équations différentielles.

Jets de fonctions entre espaces euclidiens

Avant de donner une définition rigoureuse d'un jet, il est utile d'examiner quelques cas particuliers.

Exemple : le cas unidimensionnel

Soit une fonction à valeur réelle ayant au moins k+1 dérivées dans un voisinage U du point x₀. Alors, d'après le théorème de Taylor,

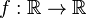
où

Alors le jet d'orde k ou k-jet de f au point x₀ est, par définition, le polynôme

Les jets sont normalement considérés comme des polynômes formels de la variable z, et pas comme de véritables fonctions de cette variable. En d'autres mots, z est une variable indéterminée qui permet d'accomplir différentes opérations algébriques sur les jets. En fait, c’est le point de base x₀ qui donne à un jet da dépendance fonctionnelle. Ainsi, en variant le point de base, un jet donne un polynôme d’ordre au plus "k" en chaque point. Ceci est une différence conceptuelle importante entre les jets et les séries de Taylor tronquées : habituellement une série de Taylor est considérée comme ayant une dépendance fonctionnelle par rapport à sa variable plutôt que par rapport à son point de base. Au contraire, les jets séparent les propriétés algébriques des séries de Taylor de leurs propriétés fonctionnelles. Nous verrons les raisons et les applications de cette séparation plus loin dans l’article.

Exemple: Applications d’un espace euclidien vers un espace euclidien

Soit une fonction d’un espace euclidien vers un autre espace euclidien, au moins (k+1) fois dérivable. Dans ce cas, le théorème de Taylor généralisé affirme que :

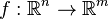
Alors, le jet d’ordre k de f est par définition le polynôme :

Exemple: Quelques propriétés algébriques des jets

Il y a deux structures algébriques basiques dont les jets sont porteurs. La première, qui finalement se révèle être la moins importante est la structure de produit. La seconde est celle de la composition des jets.

Si sont deux functions à valeurs réelles, alors le produit de leur jet peut être défini de la façon suivante :

.

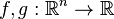
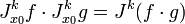
Ici, on a supprimé l’indéterminée z, car il est bien entendu que les jets sont des polynômes formels. Ce produit est simplement le produit ordinaire des polynômes en z, modulo z^{k + 1}. En d’autres termes, c’est la multiplication dans l’anneau , où (z^{k + 1}) est l’idéal engendré par les polynômes homogènes d’ordre ≥ k+1.

Considérons maintenant la composition des jets. Pour éviter des détails techniques superflus, nous considérons les jets de fonctions pour lesquelles l’image de l’origine est l’origine. Si et avec f(0)=0 et g(0)=0, alors . La composition des jets est définie par On vérifie immédiatement en utilisant la règle de dérivation des fonctions composées, que la composition des jets est une opération associative et non-commutative sur l’espace des jets à l’origine. En fait, la composition des jets d’ordre k n’est rien d’auter que la composition des polynômes modulo l’idéal des polynômes homogènes d’ordre > k.

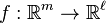
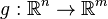
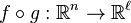
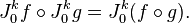
Exemples:

• En dimension 1, soit f(x) = log(1 − x) et . Alors

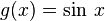
et