Isopérimétrie - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Fragments d'histoire - Résultats élémentaires - Définitions et premières propriétés - Exemples - Topologie

Topologie

À part pour le cas du quadrilatère, les théorèmes établis ne sont pas aussi puissants qu'ils y paraissent. On en prend conscience uniquement vers la moitié du XIX^e siècle. Les théorèmes indiquent que si une surface est d'aire maximale elle dessine un polygone régulier ou un disque selon le cas étudié. En revanche, ils n'indiquent pas que le polygone régulier ou bien le disque réalise ce maximum. Cette partie de la démonstration, ce chainon manquant nécessite des outils plus sophistiqués que ceux découverts à l'époque de Steiner. Ils font appel à une branche des mathématiques appelée topologie.

Tous les raisonnements présentés dans cet article, à l'exception de ceux sur le quadrilatère, ont la même structure logique. On montre qu'aucune solution n'est acceptable à l'exception d'une. Ceci ne montre pas que celle qui reste est une solution. Le mathématicien O. Perron illustre la faute logique en faisant observer qu'accepter ce type de preuve reviendrait à permettre de démontrer que 1 est le plus grand des nombres entiers. Si l'entier a est différent de 1, le carré de a est strictement plus grand que a. Le nombre a ne peut donc pas être le plus grand des entiers. L'unique exception parmi les entiers strictement positifs est 1, qui serait alors le plus grand des entiers.

Il est ainsi établi que toute surface de périmètre p et d'aire maximale ne peut être qu'un disque, mais l'énoncé n'implique pas que le disque est de fait une surface maximale, ou encore que le polygone régulier à n côtés est d'aire maximale parmi les polygones à n côtés de même périmètre. Ces deux résultats sont néanmoins vrais, les preuves associées sont proposées dans l'article Théorème isopérimétrique. Dans le cas du triangle, on peut tout de même arriver au résultat en se limitant à l'usage d'une fonction continue de la variable réelle à valeurs réelles.

Tout triangle de périmètre p et d'aire maximale est équilatéral :

Le lemme 1 montre que si un triangle n'est pas équilatéral, il ne peut être solution du problème isopérimétrique. En effet, si les trois longueurs des trois côtés sont notés a, b et c, le lemme montre que a = b et que b = c est une condition nécessaire pour que le triangle soit d'aire maximal. On en déduit qu'un tel triangle est équilatéral.

Il suffit, pour conclure de montrer qu'il existe au moins une solution.

Il existe une solution au problème isopérimétrique dans le cas des triangles :

Il faut montrer qu'il existe un triangle de périmètre p et d'aire maximale. Le lemme montre qu'il existe un triangle isocèle T_i de périmètre p et d'aire plus grande que celle du triangle initial. Il suffit donc de montrer que tout triangle isocèle de périmètre p est d'aire plus petite que celle d'un triangle T_e de périmètre p et de côté c. Soit c + 2ε la longueur de la base de T_i et c - ε la longueur des deux côtés égaux. Ici ε est un nombre réel compris entre -c /2 et c /4. La surface de T_i est le produit de la mi-longueur 1/2(c + 2ε) par la hauteur h, donnée par le théorème de Pythagore :

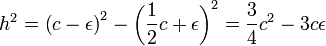
$h^2 = \left(c - \epsilon\right)^2 - \left(\frac 12 c + \epsilon\right)^2= \frac 34c^2 - 3 c\epsilon$

Si a_i est l'aire du triangle isocèle, on dispose de la formule :

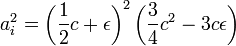
$a_i^2 = \left(\frac 12 c + \epsilon\right)^2 \left(\frac 34c^2 - 3 c\epsilon\right)$

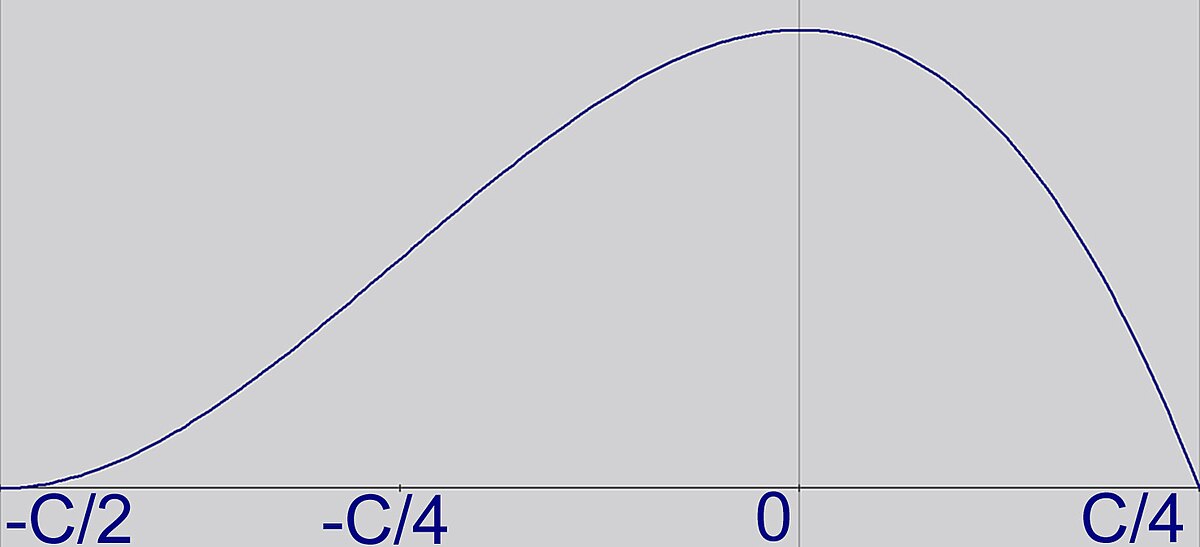
La fonction, qui à ε associe a_i² est continue, elle est illustrée sur la figure de droite. En effet, c'est un polynôme du troisième degré. Elle est définie sur un segment, le théorème des bornes nous assure que le maximum est atteint. C'est-à-dire qu'il existe au moins une solution au problème isopérimétrique pour les triangles. Graphiquement, on remarque que celle solution correspond au point ε = 0, c'est-à-dire au triangle équilatéral. Ce résultat concorde avec la proposition précédente.