Isopérimétrie - Définition

Définitions et premières propriétés

Dimension 2

Soit P_n un polygone à n côtés, où n désigne un entier plus grand que 2, p son périmètre et a_n son aire. Dans ce cas particulier, le théorème isopérimétrique s'exprime sous la forme suivante :

Ce théorème peut s'exprimer sous la forme d'une inégalité :

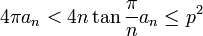
Cette propriété est très générale, elle reste vraie pour toute surface d'aire a, ayant un bord rectifiable de longueur p, c'est-à-dire que le bord est une courbe qui possède une longueur finie.

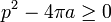
Ce théorème donne lieu à une définition :

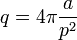
On peut interpréter ce quotient comme le carré du rapport entre le rayon du cercle ayant même aire sur le rayon du cercle ayant même périmètre. L'inégalité isopérimétrique est équivalente à dire que q est inférieur à 1, le cas d'égalité n'ayant lieu que si la surface est un disque.

Dimension 3

En dimension 3, on ne peut approcher de plus en plus précisément la sphère par des polyèdres réguliers convexes. Il n'en existe que 5, appelé solide de Platon. Le résultat général reste néanmoins vrai :

Remarque: Ici le bord du solide est une surface comme la sphère est le bord de la boule.

L'inégalité isopérimétrique s'exprime à l'aide d'un quotient isopérimétrique q. Elle indique que ce coefficient est toujours inférieur à 1 et le cas d'égalité n'a lieu que pour la sphère. Le coefficient q s'exprime sous la forme suivante, si v désigne le volume du solide et s l'aire du bord de ce solide :

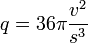
Cette formule est commentée à travers l'exemple de l'icosaèdre, à la suite de l'article.

Exemples

Les remparts d'une ville

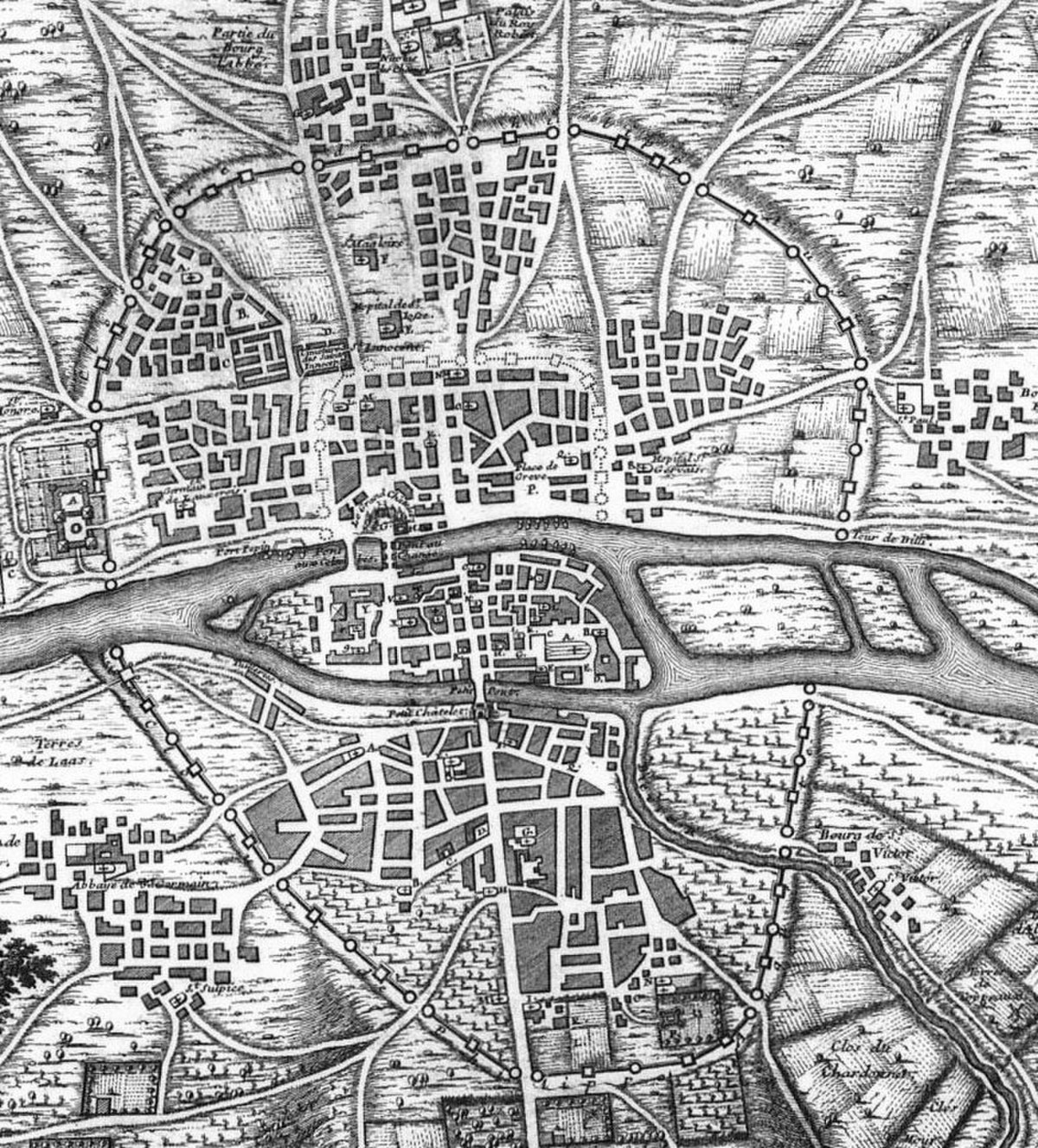
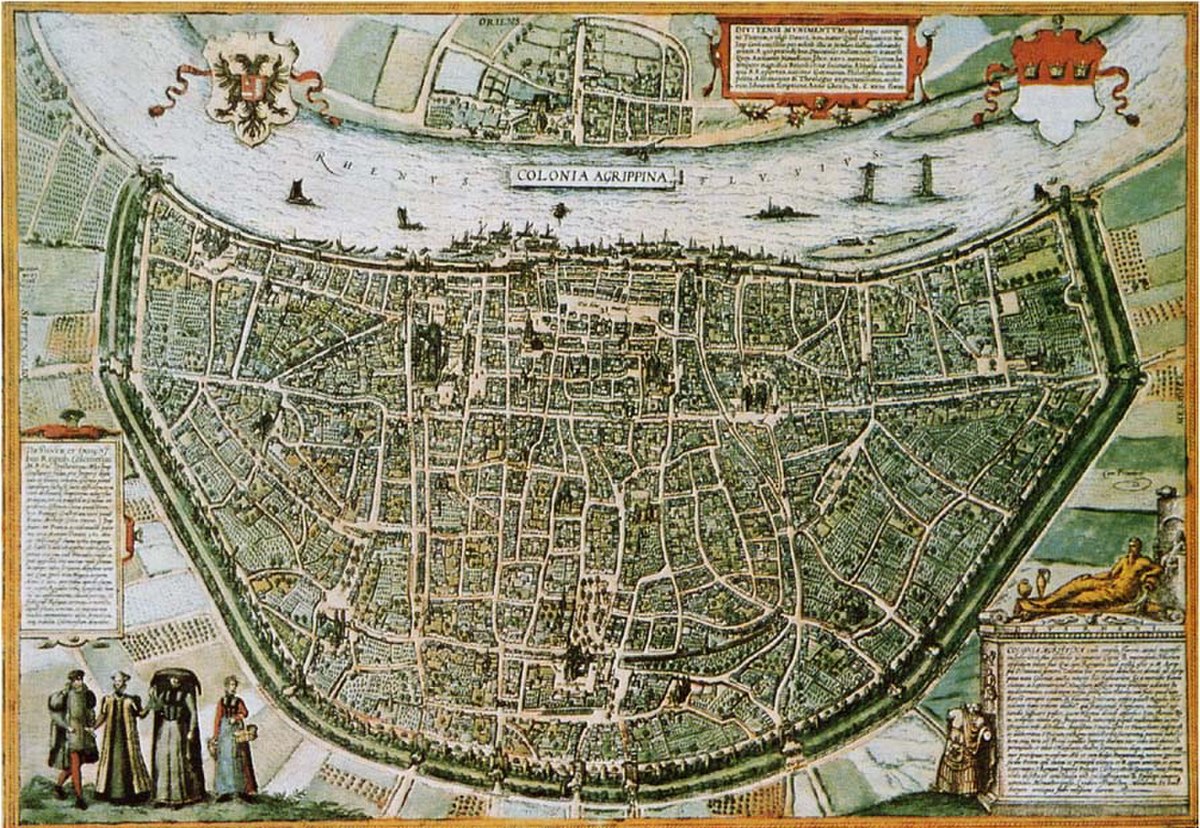
Didon n'est pas la seule dirigeante à être confrontée à la question de la plus grande surface pour un périmètre donné. Les remparts d'une ville du Moyen-Âge demandent à la fois un gros travail de construction et une soldatesque abondante pour protéger la ville en cas d'attaque. Ces deux raisons favorisent de maximiser la surface intérieure de la ville par rapport à son périmètre.

La géométrie utilisée n'est pas toujours celle du plan euclidien. Un demi plan euclidien permet par exemple d'obtenir un meilleur rapport. La solution est le demi cercle, elle est deux fois plus efficace. À l'aide d'un rempart de longueur p, on couvre une surface de p²/2π. La ville de Cologne adopte cette approche pour protéger sa ville au Moyen-Âge.

Au XVIII^e siècle d'autres contraintes favorisent une géométrie très différente. Celle de Lille par exemple, est fondée sur le principe de la tenaille, présentant des arêtes difficile à canonner de face. Elle offre une meilleure résistance à une attaque par l'artillerie.

L'œil du bouillon

L'œil dans un bouillon est constitué par une goutte d'huile en suspension dans l'eau. La surface de contact entre l'huile et l'eau est consommatrice d'énergie potentielle. L'équilibre, atteint pour le point d'énergie potentiel la plus basse est obtenue par la géométrie minimisant cette zone d'interface. Pour parler en termes imagés : « Les molécules les plus mal à l’aise se trouvent à l’interface (c’est-à-dire entre l’huile et le bouillon) donc plus l’interface est grande, plus le système est mal à l’aise ».

Pour cette raison, les gouttes adoptent une géométrie circulaire. Si deux yeux fusionnent, ils adoptent instantanément cette forme. Si un œil est coupé en deux, par exemple à l'aide d'un couteau, les deux yeux obtenus reprennent aussi une forme circulaire.

Cette même cause impose aux bulles de savon de taille pas trop vaste, une forme sphérique. L'énergie potentielle est maximale si la surface de la bulle est minimale, la bulle a tendance à enfermer le volume d'air dans un espace sphérique, car il minimise au mieux la surface, pour un volume donné (celui de l'air emprisonné).

L'icosaèdre

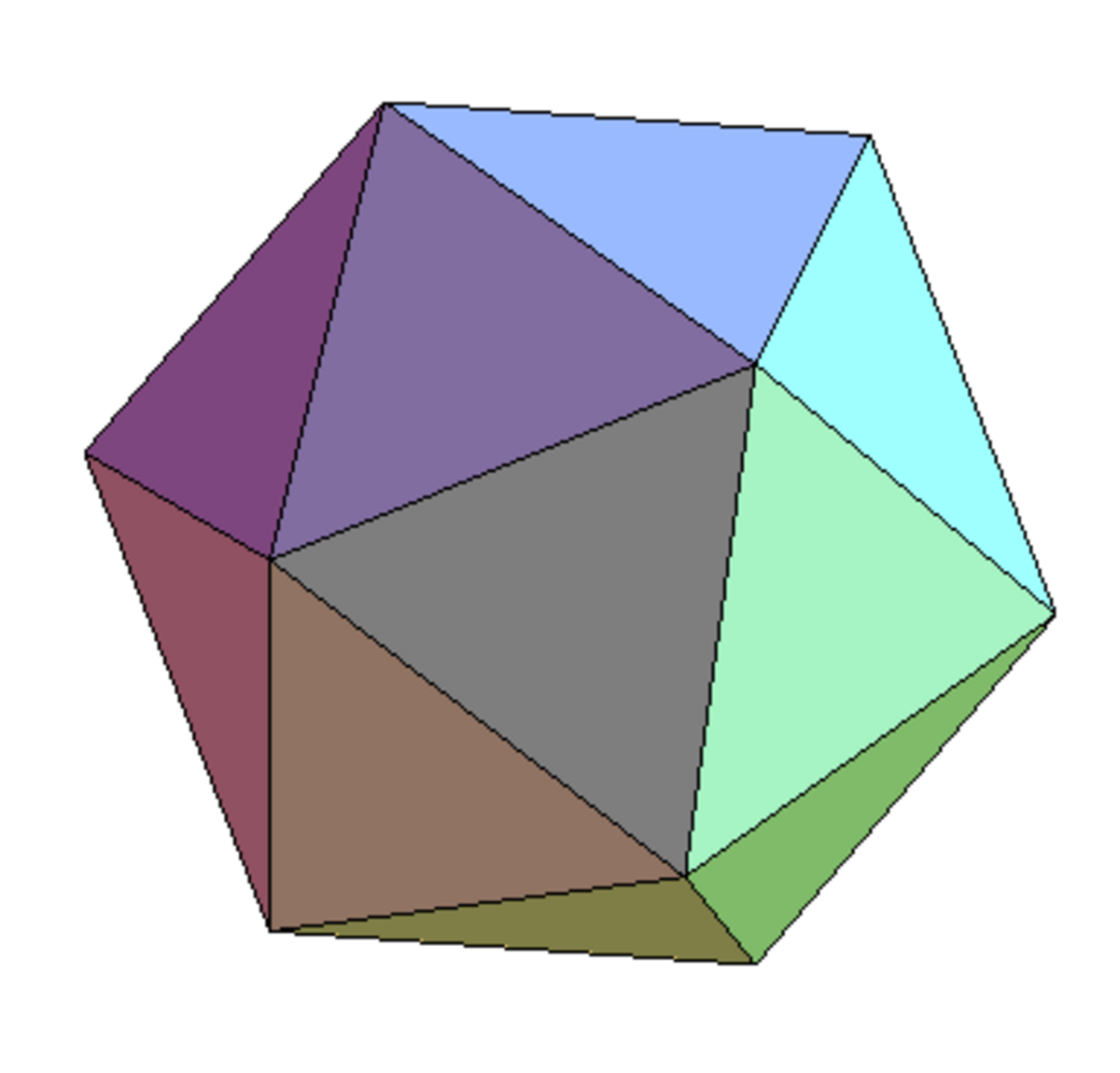
Le théorème d'isopérimétrie indique que, pour tout solide mesurable, de surface mesurable, le volume est plus petit que celui d'une sphère de même surface. Ainsi un solide de surface S possède toujours un volume V inférieur à V_s, celui d'une sphère de même surface :

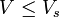
La sphère de rayon r possède une surface de 4πr², le rayon r de la sphère en question est égal à √S/2√π. Le volume V_s est égal à 4πr³/3. On en déduit une nouvelle majoration :

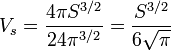
La formule s'exprime plus simplement si elle est mise au carré, on obtient :

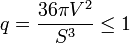
Ce qui donne une forme d'inégalité isopérimétrique et la formule du quotient isopérimétrique, noté ici q. Dans le cas d'un icosaèdre, et si a désigne l'arête du solide, on dispose des formules suivantes :

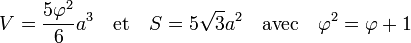
Ici, φ désigne le nombre d'or égal à 1/2(1 + √5). On trouve :

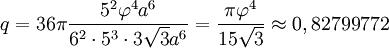
Ce quotient isopérimétrique est la valeur la plus élevée possible pour un solide de Platon.