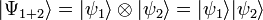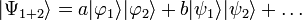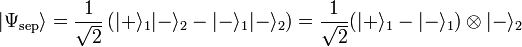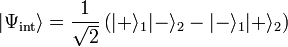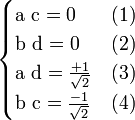Intrication quantique - Définition

Implications philosophiques

Indubitablement, le fait que la mécanique quantique tolère l'existence d'états intriqués, états ayant effectivement été observés en laboratoire et dont le comportement est en accord avec celui prévu par la mécanique quantique, implique que la mécanique quantique est une théorie physique non-locale.

Par contre, la mécanique quantique est bien compatible avec la théorie de la relativité, car on démontre que les états intriqués ne peuvent pas être utilisés pour transmettre une information quelconque d'un point à un autre de l'espace-temps plus rapidement qu'avec de la lumière. La raison est que le résultat de la mesure relatif à la première particule est toujours aléatoire, dans le cas des états intriqués comme dans le cas des états non-intriqués : il est donc impossible de « transmettre » quelque information que ce soit, puisque la modification de l'état de l'autre particule, pour instantanée qu'elle soit, conduit à un résultat de la mesure relatif à la seconde particule qui est toujours aussi aléatoire que celui relatif à la première particule ; les corrélations entre les mesures des deux particules resteront indétectables tant que les résultats des mesures ne seront pas comparés, ce qui implique nécessairement un échange d'information classique, respectueux de la relativité. Par suite, la mécanique quantique est bien également parfaitement compatible avec le principe de causalité.

Définition

Il est plus aisé de définir ce qu'est un état non intriqué, ou séparable, que de définir directement ce qu'est un état intriqué.

État pur

Dans le cas où le système global {S₁+S₂} peut être décrit par un vecteur d'état, son état est un vecteur de l'espace de Hilbert . Certains états peuvent s'écrire sous la forme d'un produit tensoriel entre un état de S₁ et un état de S₂ :

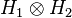
Ces états sont appelés états séparables ou factorisables. Le système S₁ est dans un état quantique clairement identifié, , qui n'est pas altéré par les mesures effectuées sur S₂.

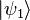
Un état intriqué est par définition un état non séparable, qui s'écrit en général sous la forme

C'est donc une superposition d'états d'un système bipartite. Pour illustrer la différence entre états séparables et intriqués, supposons par exemple que forme une base de l'espace H₁, et une base de l'espace H₂. L'état :

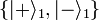
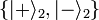
est un état séparable, puisqu'il peut être factorisé comme indiqué ci-dessus, tandis que l'état :

est un état intriqué.

Si était un état factorisable, on devrait pouvoir l'écrire sous la forme générale :

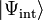
où a, b, c et d sont quatre nombres complexes. Dans le second membre, le premier terme représenterait l'état du sous-système S₁ dans l'espace H₁, et le second terme représenterait l'état du sous-système S₂ dans l'espace H₂. On obtient alors le système suivant :

Pour que l'équation (1) soit vérifiée, il est nécessaire soit que a = 0, ce qui est incompatible avec (3), soit que c = 0, ce qui est incompatible avec (4). Le système ci-dessus n'a donc pas de solution, montrant que l'état n'est pas factorisable.

 

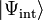
Par suite, il existe des états a priori légitimes d'un système global {S₁ + S₂} qui ne peuvent pas s'écrire sous la forme du produit tensoriel d'un état d'un sous-système S₁ par un état d'un sous-système S₂ ; pour de tels états intriqués, il est donc impossible de parler de « l'état de S₁ » : seul le système global {S₁ + S₂} a un état défini, état défini par le premier membre de la relation ci-dessus. En un sens, il n'est plus possible de séparer conceptuellement les deux systèmes.

La principale caractéristique de l'état est qu'il y a corrélation parfaite des mesures réalisées sur S₁ avec les mesures réalisées sur S₂. Ainsi, supposons que l'on mesure l'état de S₁ dans la base « +/– » et que l'on trouve « + » (ce qui peut arriver aléatoirement dans 50% des cas). Le système total {S₁+S₂} est alors projeté dans l'état , de sorte que la mesure de S₂ donnera "–" avec certitude, même si les deux mesures sont séparées par un intervalle de genre espace dans l'espace-temps. Einstein décrivait ce phénomène comme une « action surnaturelle à distance », car tout se passe comme si la mesure effectuée sur S₁ à un instant donné avait un effet absolument instantané sur le résultat de la mesure effectuée sur S₂ même si les deux événements ne sont pas reliés causalement, c'est-à-dire même si une information partant de S₁ et se déplaçant à la vitesse de la lumière n'a pas le temps d'informer S₂ du résultat de la mesure sur S₁. De fait, un système intriqué forme absolument un tout, qui ne peut pas être séparé en deux systèmes indépendants tant qu'il reste intriqué, quelle que soit l'étendue spatiale de ce système. Voir ci-dessous les conséquences philosophiques que cela peut avoir, ainsi que l'article relatif au paradoxe EPR et celui relatif à l'expérience d'Aspect au cours de laquelle des états intriqués d'un système de deux photons ont été produits en laboratoire pour la première fois, chaque photon représentant l'un des deux sous-systèmes S₁ et S₂ du système global {S₁ + S₂} constitué par l'ensemble des deux photons.

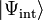
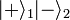
État mixte

Expérimentalement, il n'est pas possible de préparer un état quantique bien déterminé avec une reproductibilité de 100%. Pour tenir compte de cette préparation imparfaite, on décrit l'état du système par une matrice densité, qui pondère chaque état pur par la probabilité de produire cet état : . On peut donc se demander quelle est la définition d'un état séparable décrit par une matrice densité. Un premier choix serait de définir les états séparables comme étant ceux qui s'écrivent :

.

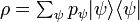
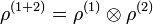
Ces états sont effectivement séparables, car il n'y a aucune corrélation entre les mesures faites sur S₁ et celles faites sur S₂, mais la définition peut être étendue, et l'écriture la plus générale pour la matrice densité d'un état séparable est :

,

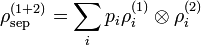
où p_i est une loi de probabilité (p_i > 0 et ).

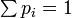
Cette définition présente l'avantage d'inclure les systèmes corrélés classiquement dans les états séparables. Supposons par exemple une expérience qui produise deux particules simultanément, et aléatoirement une fois sur deux un état , et une fois sur deux un état . L'état ainsi produit est représenté par la matrice . Alternativement, on peut imaginer un physicien facétieux qui envoie chaque jour deux lettres, l'une contenant un signe « + » et l'autre contenant un signe « – », à deux de ses collègues (1 et 2), mais en faisant correspondre aléatoirement les lettres et les adresses. Les mesures réalisées sur S₁ seront parfaitement corrélées à celles réalisées sur S₂ : si la mesure donne « + » pour un système, on est sûr que la mesure de l'autre système donnera « – ». Cependant, ces corrélations ne sont pas de nature quantiques : elles existent dès la production des deux particules et ne proviennent pas du fait que l'on mesure l'état du système. En particulier, si l'on changeait de base de mesure en utilisant une observable ne commutant pas avec l'observable « signe », on s'apercevrait que l'état ainsi produit ne viole pas les inégalités de Bell. Les résultats sont donc différents de ceux obtenus avec l'état intriqué décrit précédemment.

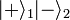
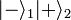
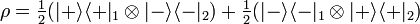
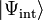
Dans le formalisme de la matrice densité, un état intriqué est simplement défini comme un état qui n'est pas séparable. Dans le cas général, même lorsque l'on connaît la matrice densité d'un système, il est difficile de dire si l'état obtenu est intriqué ou séparable. Une condition nécessaire est de regarder si la « transposée partielle » de la matrice densité est positive. Pour les dimensions 2 et 3, cette condition est également suffisante.