Intervalle d'espace-temps - Définition

Cas de l'invariance comme hypothèse

Si l'invariance du le carré de l'intervalle d'espace-temps, par changement de référentiel, est posée comme hypothèse initiale dans la théorie de la relativité, les déductions qui en sont faites sont alors mathématiquement cohérentes avec la théorie, mais certaines doivent être écartées pour des raisons physiques.

En relativité restreinte

Identifier l'espace physique à un espace mathématique à quatre dimensions doté d'une semblable distance (on dit aussi pseudo-norme) amène à identifier les repères de l'espace affine à quatre dimensions et les référentiels inertiels de la physique, et en cherchant tous les changements de repère ayant la propriété de laisser invariant l'intervalle d'espace-temps, on en trouve qui, tout en étant cohérents avec les mathématiques de la théorie relativiste, ne peuvent être retenus comme des changements de référentiel physiquement réalistes car ils ne respectent pas la convention d'orientation des repères tridimensionnels (l'orientation unanimement admise étant celle de la main droite) ou celle de l'orientation de l'axe du temps (vers le futur).

Les transformations qui préservent les orientations de l'espace et du temps sont les transformations de Lorentz établies dès l'origine par Lorentz, et sont appelées, dans le cadre de cette problématique, transformations de Lorentz propres et orthochrones. Les autres transformations ne sont pas utilisées en physique relativiste mais le sont en physique quantique relativiste pour exploiter les symétries mathématiques des équations. Par exemples, la symétrie T et la parité sont interprétées comme de simples changements de convention des orientations des axes de coordonnées spatiales et temporelle. Ainsi, la symétrie P change-t-elle la convention du choix des référentiels par la main droite en convention du choix par la main gauche.

En relativité générale

En relativité générale, l'espace-temps étant essentiellement structuré par l'algèbre, il faut prendre garde à écarter les hypothèses ou résultats mathématiquement corrects mais physiquement irréalistes. Cela est vrai en particulier pour le carré de l'intervalle d'espace-temps qui est un élément fondateur de la théorie (du point de vue mathématique) du fait de son invariance par changement de référentiel et de son lien avec la gravitation (qui est une manifestation de la courbure). Déjà, les g_μν forment une matrice qui doit avoir un déterminant négatif pour avoir un sens physique.

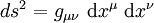
Ainsi, dans un référentiel réalistepour un observateur, si la coordonnée x₀ correspond à la mesure du temps et les coordonnées x₁;x₂;x₃ correspondent à un référentiel spatial quelconque, les termes g_μν doivent vérifier g₀₀ > 0, ainsi que g_kk < 0 pour k=1, 2, 3 (bref : la signature doit rester inchangée par rapport à celle de la métrique de Minkowski)..

Mais la relativité générale autorise l'utilisation de n'importe quel système de référence dans cet espace à quatre dimensions, sans l'obligation de ce préoccuper de réalisme, comme méthode mathématique pour déterminer des propriétés de l'espace-temps, et dans ce cas les coefficients g_μν ne sont pas soumis à ces contraintes.

Métrique

L'espace-temps de la relativité restreinte est doté par le carré de l'intervalle d'espace-temps d'une sorte de distance qui est invariante par changement de référentiel. Vu de cet manière, l'intervalle d'espace-temps peut être considéré comme une métrique de l'espace, à partir de la quelle se démontrent nombres de propriétés mathématiques de l'espace et de la théorie relativiste.

Lorsque les deux événements A et B entre lesquels on calcule le carré de l'intervalle d'espace-temps sont très voisins, leurs coordonnées ne différent donc que par les quantités infinitésimales . Cette considération est superflue en relativité restreinte dont l'espace est affine, mais est indispensable en relativité générale dont l'espace est une variété courbe où les ne peuvent être définis avec rigueur, mais où les éléments infinitésimaux (dx^μ) sont définissables et appartiennent à l'espace tangent.

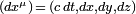
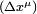
En relativité restreinte, le carré de l'intervalle infinitésimal d'espace-temps s'écrit alors : .

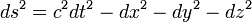
La métrique de la relativité générale est définissable à partir de celle de la relativité restreinte, en tenant compte du principe d'équivalence et du principe de relativité généralisé à tous les référentiels, et c'est un élément de base (d'un point de vue mathématique) pour la construction de cette théorie. Elle permet la définition de l'élément infinitésimal du le carré de l'intervalle d'espace-temps dans cette théorie.

En relativité générale, la formule du carré de l'intervalle infinitésimal d'espace-temps est , où les coefficients de la métrique, g_μν, varient d'un point à l'autre de l'espace-temps, en fonction de la courbure de l'espace.

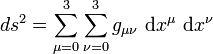
On écrit aussi, avec la convention d'Einstein pour les sommation : .

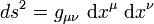
Mais cette définition à partir d'éléments infinitésimaux et la courbure de l'espace-temps rendent délicats la justification de propriétés similaires à celles exposées dans les paragraphes ci-dessus, mis à part localement. Toutefois, à partir d'un événement O, on peut toujours faire la partition de l'espace-temps dans son ensemble en événements liés à O par une géodésique de genre temps, lumière ou espace (le genre correspondant au signe constant de ds² le long de la géodésique).