Intégrale de chemin - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Genèse du concept d'intégrale de chemin - Expression du propagateur en termes d'intégrale de chemin - Rappels sur le propagateur de l'équation de Schrödinger - Bibliographie - Limite semi-classique

Introduction

Une intégrale de chemin («path integral» en anglais) est une intégrale fonctionnelle, c'est-à-dire que l'intégrant est une fonctionnelle et que la somme est prise sur des fonctions, et non sur des nombres réels (ou complexes) comme pour les intégrales ordinaires. On a donc ici affaire à une intégrale en dimension infinie. Ainsi, on distinguera soigneusement l'intégrale de chemin (intégrale fonctionnelle) d'une intégrale ordinaire calculée sur un chemin de l'espace physique, que les mathématiciens appellent intégrale curviligne.

C'est Richard Feynman qui a introduit les intégrales de chemin en physique dans sa thèse, soutenue en mai 1942, portant sur la formulation de la mécanique quantique basée sur le lagrangien. En raison de la Seconde Guerre mondiale, ces résultats ne seront publiés qu'en 1948. Cet outil mathématique s'est rapidement imposé en physique théorique avec sa généralisation à la théorie quantique des champs, permettant notamment une quantification des théories de jauge non-abéliennes plus simple que la procédure de quantification canonique.

Par ailleurs, le mathématicien Mark Kac a ensuite développé un concept similaire pour la description théorique du mouvement brownien, s'inspirant de résultats obtenus par Norbert Wiener dans les années 1920. On parle dans ce cas de la formule de Feynman-Kac, qui est une intégrale pour la mesure de Wiener.

Genèse du concept d'intégrale de chemin

Alors qu'il est étudiant de 3^e cycle sous la direction de Wheeler à l'université de Princeton, le jeune Feynman cherche une méthode de quantification basée sur le lagrangien pour pouvoir décrire un système ne possédant pas nécessairement d'hamiltonien. Sa motivation première est de quantifier la nouvelle formulation de l'électrodynamique classique basée sur l'action à distance qu'il vient juste de développer avec Wheeler.

Au printemps de 1941, il rencontre Herbert Jehle, alors visiteur à Princeton, qui lui indique lors d'une soirée à la Nassau Tavern l'existence d'un article de Dirac qui discute précisément la quantification à partir du lagrangien. Jehle précise à Feynman que cette formulation permet une approche relativiste covariante bien plus aisée que celle basée sur le hamiltonien. Le lendemain, les deux physiciens se rendent à la bibliothèque pour étudier l'article de Dirac. Ils y lisent notamment la phrase suivante : pour deux instants $t\,$ et $t + \epsilon\,$ voisins, l'amplitude de transition élémentaire :

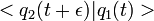$< q_2(t + \epsilon) | q_1(t) > \,$ est analogue à

Dans cette formule, la grandeur $S[q(t)]\,$ est l'action classique :

Afin de comprendre ce que Dirac veux dire par analogue, Feynman étudie le cas d'une particule non relativiste de masse $m\,$ pour laquelle le lagrangien s'écrit :

On sait que :

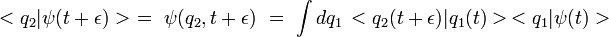$< q_2 | \psi(t+\epsilon) > \ = \ \psi(q_2,t + \epsilon)\ = \ \int dq_1 \, < q_2(t + \epsilon) | q_1(t) > \, < q_1 | \psi(t) >$

Feynman suppose alors une relation de proportionnalité :

où $A\,$ est une constante inconnue. En présence de Jehle, Feynman démontre que cette équation implique que $\psi(q,t)\,$ obéit à l'équation de Schrödinger :