Infini - Définition

Introduction

Le

Le mot « infini » (-e, -s ; du latin finitus, « limité »), est un adjectif servant à qualifier quelque chose qui n'a pas de limite en nombre ou en taille.

En mathématiques

On rencontre les grandeurs infinies dans plusieurs branches des mathématiques, sous le double aspect du nombre par la théorie des cardinaux et de l'espace par la théorie de la mesure. Ces deux aspects ne se recouvrent pas nécessairement, ainsi un segment ou un disque ont une infinité de points mais une mesure finie.

En théorie des ensembles

Un ensemble E est infini si, et seulement si, il n'est équipotent à aucun intervalle borné de N, ou de façon équivalente, s'il existe au moins une famille non vide de sous-ensembles de E qui n'a pas d'élément minimal pour l'inclusion.

Ensembles infinis dénombrables

Un ensemble infini est dit dénombrable si, et seulement si, il existe une bijection entre lui et N. Intuitivement, un ensemble infini est dénombrable si, et seulement si, on peut « énumérer » ses éléments: le « premier » élément, le « deuxième » élément, le « troisième » élément, et ainsi de suite sans s'arrêter.

Par exemple, nous pouvons montrer que Q⁺ est dénombrable, voir la méthode.

L'ensemble N² = N x N des couples d'entiers naturels est lui aussi dénombrable, car à tout couple (p,q), on peut associer le nombre n = [(p+q)(p+q+1)/2] + p, et on vérifiera aisément que la fonction ainsi définie est injective.

Dans l'exemple ci-dessus l'énumération des couples est « effective » : le procédé d'énumération est un procédé calculatoire, un algorithme. Mais on peut très bien avoir montré qu'un ensemble est infini dénombrable, par exemple en montrant qu'il est sous-ensemble des entiers et ne peut être fini, sans être capable de donner un procédé effectif d'énumération. Cette dernière notion est étudiée dans l'article ensemble récursivement énumérable.

Si l'on admet l'axiome du choix, et seulement à cette condition, tout ensemble E est en correspondance biunivoque avec un ordinal ; le plus petit ordinal auquel E est équipotent est alors par définition le cardinal de E.

Le cardinal d'un ensemble fini est un nombre entier naturel.

Le cardinal d'un ensemble infini est dit « transfini ». Le cardinal (on parle aussi de « puissance ») des ensembles infinis dénombrables est noté (« aleph-zéro »).

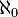
Ensembles infinis non dénombrables

Un ensemble infini non dénombrable ne peut pas être mis en bijection avec N. On ne peut pas établir une liste de ses éléments.

Ainsi en est-il de l'ensemble des nombres réels. Les nombres réels forment un corps commutatif totalement ordonné R, archimédien et tel que toute partie majorée admette une borne supérieure ; R est l'unique corps, à l'isomorphisme près, à satisfaire ces propriétés ; c'est le sur-corps minimal de Q à satisfaire le critère de Cauchy.

L'ensemble des réels compris entre 0 et 1 est déjà non dénombrable : la démonstration s'appuie sur l'argument de la diagonale de Cantor.

On dit que R a la puissance du continu, sa puissance (ou son cardinal) est , le cardinal de l'ensemble des parties de N. L'argument diagonal de Cantor montre du même coup que , le plus petit cardinal non dénombrable, est inférieur ou égal à (dans ZFC). L'égalité de ces deux cardinaux, que l'on appelle l' hypothèse du continu, est indépendante des axiomes de la théorie des ensembles ZFC.

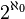
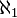
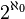
En géométrie

Les peintres de la Renaissance, cherchant une représentation du réel qui soit fidèle à notre perception, développèrent les méthodes de représentation perspective. Des lignes horizontales parallèles « se coupent à l'infini » dans l'espace et en un point sur le tableau; ce point du tableau ainsi que la ligne d'horizon du tableau correspondent à une certaine réalité en deux dimensions (2D).

La géométrie projective consiste à rajouter à l'espace affine usuel des points dits « à l'infini » dans chaque direction. Le but est de ne plus faire de distinction entre droites sécantes et droites parallèles, ces dernières ayant un point commun à l'infini. C'est un outil de simplification remarquable. À titre d'exemple, en géométrie projective, il n'existe qu'un seul type de coniques au lieu de trois.

En optique géométrique

• Un objet situé « à l'infini » est une source émettant des rayons lumineux parallèles,
• Une image se forme « à l'infini » quand les rayons lumineux qui la forment sont parallèles.

Un œil normal (emmétrope) ou corrigé doit voir nettement une image à l'infini (Punctum remotum).

En topologie

compactification

L'ajout d'un élément ∞ à un espace topologique localement compact permet de rendre cet espace compact. Il s'agit de la compactification d'Alexandroff.

Soit un espace topologique localement compact, son compactifié est l'espace , où est un élément extérieur à E, et U' est obtenu de U en lui ajoutant tous les complémentaires dans des compacts de .

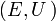
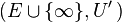
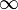
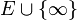
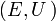
On peut alors définir les « voisinages de l'infini » : il s'agit de toute partie contenant un ouvert de U'\ U.

complétion

On peut compléter le corps des nombres réels, en sacrifiant sa propriété de corps, usuellement de deux manières possibles :

• soit en le complétant du point de vue algébrique par l'ajout d'un élément ∞, qui devient formellement un inverse de 0. C'est un point fixe de l'addition et du produit en ce sens que (∀x∈ R)  x ≠ 0 ⇒  ∞ + x = ∞ ∧ ∞ × x = ∞. Par contre, le produit ∞ × 0 n'est pas défini.

On obtient ainsi l'espace projectif à 1 dimension. Dans cette complétion, le corps des réels perd son caractère ordonné. On peut lui assigner la topologie de compactification d'Alexandroff des réels, par la méthode précédente, ce qui lui confère la même structure topologique que la circonférence.

• par l'ajout de deux éléments +∞ (on omet le signe + si on ne risque pas de confusion avec ce qui précède) et -∞. On considère que +∞ est plus grand que tout nombre réel et que -∞, et que -∞ est plus petit que tout autre élément y compris +∞. L'ensemble ainsi obtenu est totalement ordonné, mais perd sa structure de corps, ainsi que ses propriétés algébriques. Du point de vue topologique, c'est un espace compact, pour une topologie respectant sa structure d'ordre. Cela lui confère la même topologie qu'un intervalle fermé, par exemple [-1,1].