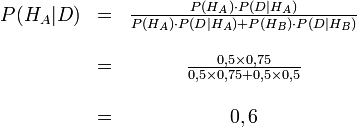Inférence bayésienne - Définition

Exemples d'inférence bayésienne

D'où vient ce biscuit ?

(cet exemple est tiré de l'article anglophone)

Imaginons deux boîtes de biscuits.

• L'une, A, comporte 30 biscuits au chocolat et 10 ordinaires.
• L'autre, B, en comporte 20 de chaque sorte.

On choisit les yeux fermés une boîte au hasard, puis dans cette boîte un biscuit au hasard. Il se trouve être au chocolat. De quelle boîte a-t-il le plus de chances d'être issu, et avec quelle probabilité ? Intuitivement, on se doute que la boîte A a plus de chances d'être la bonne, mais de combien ?

La réponse exacte est donnée par le théorème de Bayes :

Notons H_A la proposition « le gâteau vient de la boîte A » et H_B la proposition « le gâteau vient de la boîte B ».

Si lorsqu'on a les yeux bandés les boîtes ne se distinguent que par leur nom, nous avons P(H_A) = P(H_B), et la somme fait 1, puisque nous avons bien choisi une boîte, soit une probabilité de 0,5 pour chaque proposition.

Notons D l'événement désigné par la phrase « le gâteau est au chocolat ». Connaissant le contenu des boîtes, nous savons que :

• P(D | H_A) = 30/40 = 0,75 (évidence 4,77 dB, soit 1,44 bit)
• P(D | H_B) = 20/40 = 0,5 (évidence 0 dB, soit 0 bit)

Note: « P(A | B) » se dit « la probabilité de A sachant B ».

Résolution

La formule de Bayes nous donne donc :

P(H_A|D) représente la probabilité d'avoir choisi la boîte A sachant que le gâteau est au chocolat.

Avant de regarder le gâteau, notre probabilité d'avoir choisi la boîte A était P(H_A), soit 0,5.

Après l'avoir regardé, nous révisons cette probabilité à P(H_A|D), qui est 0,6 (1,76 dB ou 0,53 bit).

L'observation nous a donc apporté 1,76 dB (0,53 bit).

Et puisque P(H_A|D) + P(H_B|D) = 1 (pas d'autre possibilité que d'avoir choisi la boîte A ou la boîte B sachant que le gâteau est au chocolat), la probabilité d'avoir choisi la boîte B sachant que le gâteau est au chocolat est donc de 1 - 0,6 = 0,4

Si nous imposons une probabilité a priori quelconque de suspecter une boîte particulière plutôt que l'autre, le même calcul effectué avec cette probabilité a priori fournit également 0,53 bit. C'est là une manifestation de la règle de cohérence qui constituait l'un des desiderata de Cox.

Où en sont les immatriculations du moment ?

Supposons qu'un pays numérote les plaques minéralogiques de ses véhicules de 1 en 1 en partant de 1. Nous observons N plaques portant des numéros S₁, ... S_N. Pour N supérieur à 3, on démontre par la méthode de Bayes que le meilleur estimateur du numéro en cours K ne dépend que de N et de la plus haute immatriculation trouvée S_max, selon la formule suivante :

K = S_max x (N-1)/(N-2)

Plus intéressant encore, la variance de cette estimation devient exponentiellement petite avec la valeur de N. La démonstration est donnée dans Tribus, Décisions rationnelles dans l'incertain.

Comparaison avec la statistique classique

Différence d'esprit

Une différence entre l'inférence bayésienne et les statistiques classiques, dites aussi fréquentistes, indiquée par Myron Tribus, est que

• les méthodes bayésiennes utilisent des méthodes impersonnelles pour mettre à jour des probabilités personnelles, dites aussi subjectives (une probabilité est en fait toujours subjective, lorsqu'on analyse ses fondements),
• les méthodes statistiques utilisent des méthodes personnelles pour traiter des fréquences impersonnelles.

Les bayésiens font donc le choix de modéliser leurs attentes en début de processus (quitte à réviser ce premier jugement à l'aune de l'expérience au fur et à mesure des observations), tandis que les statisticiens classiques se fixaient a priori une méthode et une hypothèse arbitraires et ne traitaient les données qu'ensuite (ce qui avait tout de même le mérite de bien alléger les calculs).

Les méthodes bayésiennes, parce qu'elles n'exigeaient pas qu'on se fixe d'hypothèse préalable, ont ouvert la voie au data mining automatique; il n'y a en effet plus lieu avec elles d'avoir recours à une intuition humaine préalable pour imaginer des hypothèses avant de pouvoir commencer à travailler.

Quand utiliser l'une ou l'autre ?

Les deux approches se complètent, la statistique étant en général préférable lorsque les informations sont abondantes et d'un faible coût de collecte, la bayésienne dans le cas où elles sont rares et/ou onéreuses à rassembler. En cas de profusion de données, les résultats sont asymptotiquement les mêmes dans chaque méthode, la bayésienne étant simplement plus coûteuse en calcul. En revanche, la bayésienne permet de traiter des cas où la statistique ne disposerait pas suffisamment de données pour qu'on puisse en appliquer les théorèmes limites.

Le psi-test bayésien (qui est utilisé pour déterminer la plausibilité d'une distribution par rapport à des observations) est asymptotiquement convergent avec le χ² des statistiques classiques à mesure que le nombre d'observations devient grand. Le choix apparemment arbitraire d'une distance euclidienne dans le χ² est ainsi parfaitement justifié a posteriori par le raisonnement bayésien (source : Myron Tribus, op. cit.)