Inégalités de Bell - Définition

Inégalité faible et inégalité forte

Il est remarquable que selon la théorie, avec des instruments performants à 100% on aurait théoriquement une corrélation absolue entre les particules intriquées. Or cela est simplement impossible à vérifier technologiquement. Les inégalités de Bell dans leur formulation initiale étaient impossibles à vérifier avec un appareillage réel. Des éléments comme la disposition des polariseurs, filtres et détecteurs devaient fausser les résultats des expériences. Pour pouvoir faire une expérience réalisable techniquement, il était donc nécessaire d'intégrer dans les calculs initiaux de Bell la marge d'erreurs induites par l'appareil expérimental. Il existe des polarisateurs et des filtres opérant avec une efficacité de 95 à 98%, l'efficacité des photomultiplicateurs étant de l'ordre de 10 à 20%, il fallait donc tenir compte de ces limites technologiques lors des expériences. C'est ainsi que, pour pouvoir tester l'inégalité de Bell avec l'imperfection des techniques réalistes, des hypothèses additionnelles de CHSH (en) et de CH74 inequality (en) furent introduites dans les expériences pour transformer les inégalités faibles de Bell ne pouvant être vérifiés qu'avec des instruments parfaits, en inégalités fortes enfin vérifiables avec des instruments réels. Inégalités fortes qui furent systématiquement violées par les expériences et confirmant les prédictions quantiques.

La mécanique quantique

Dans le cas de la mécanique quantique, si l'angle du premier polariseur est α et l'angle du deuxième polariseur est β, alors le calcul (identique à la probabilité de mesurer le spin selon l'angle α alors que l'on sait que le spin a été mesuré selon l'angle β) donne :

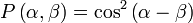
Comme on mesure des coïncidences, la fonction de corrélation est alors donnée par :

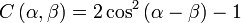
On voit que les inégalités de Bell sont violées pour, par exemple, des angles égaux à , et .

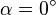
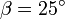
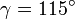
L'expérience (par exemple celle d'Alain Aspect) a largement confirmé ces résultats et aussi que la loi de Malus était vérifiée sur des photons individuels.

Bibliographie

Travaux originaux

• J. S. Bell, On the Einstein Podolsky Rosen Paradox, Physics 1 (1964), 195.

• J. S. Bell, On the problem of hidden variables in quantum mechanics, Review of Modern Physics 38 (1966), 447.

• J. S. Bell, Introduction to the hidden variable question, Proceedings of the International School of Physics Enrico Fermi, Course IL, Foundations of Quantum Mechanics (1971), 171-181.

• J. S. Bell, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press (1987), ISBN

• M. Bell, K. Gottfried & M. Veltman ; John S Bell on the foundations of quantum mechanics, World Scientific (2001), ISBN 981-02-4688-9.

Autres références

• Banesh Hoffmann, Michel Paty, L'étrange histoire des quanta, Editions du seuil, 1981.

• Alain Aspect ; Quelques tests expérimentaux des fondements de la mécanique quantique (en optique), Qu'est-ce que l'Univers ?, Vol. 4 de l'Université de Tous les Savoirs (sous la direction d'Yves Michaux), Odile Jacob (2001), ISBN 2-7381-0917-9, pp. 589. Dualité onde-corpuscule, intrication quantique & paradoxe EPR expliqués par un professeur d'optique à l'Université de Paris-Sud (Orsay), auteur en 1982 d'une expérience testant les inégalités de Bell.
• Alain Aspect ; Bell's Theorem : The naive view of an experimentalist, conférence en mémoire de John Bell (Vienne, Décembre 2000). Publié dans : R. A. Bertlmann et A. Zeilinger (eds.) ; Quantum [un]speakables - From Bell to quantum information, Springer (2002). Texte complet disponible sur l'ArXiv : quant-ph/0402001.

• R. Jackiw, A. Shimony ; The depth and breadth of John Bell's physics, Phys.Perspect. 4 (2004) 78-116. Texte complet disponible sur l'ArXiv : physics/0105046.

• Asher Peres ; All the Bell inequalities, Foundations of Physics 29 (1999) 589-614. Texte complet disponible sur l'ArXiv : quant-ph/9807017.

• H. M. Wiseman ; From Einstein's theorem to Bell's theorem: a history of quantum nonlocality, Contemporary Physics 47, 79-88 (2006) ; texte complet disponible sur l'ArXiv : quant-ph/0509061 (Septembre 2005).