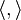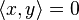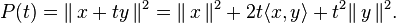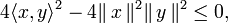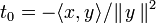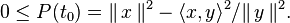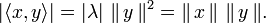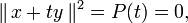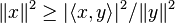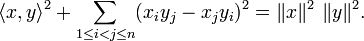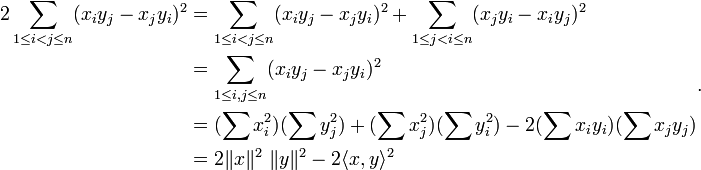Inégalité de Cauchy-Schwarz - Définition

Démonstrations

Les démonstrations présentées ici sont valables aussi bien dans le cadre d'un espace préhilbertien complexe que réel, sauf bien sûr la dernière.

Lorsque y=0, l'énoncé est clairement vrai, par conséquent on supposera y non nul.

En outre, pour la première démonstration, qui est la plus connue, on suppose que le nombre est réel. On obtient la généralisation du cas étudié par multiplication du vecteur x (ou y) par un nombre complexe convenable de module égal à 1. Ceci étant devient réel sans changer de module; et ne varient pas non plus.

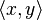
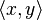
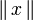
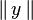
Inégalité

Posons, pour tout réel t,

Par construction, cette expression polynomiale du second degré est positive ou nulle pour tout réel t. On en déduit que son discriminant est négatif ou nul :

d'où l'inégalité annoncée.

Une variante plus directe est de poser

et d'utiliser que

(Ce t₀ n'est autre que la valeur en laquelle P atteint son minimum, mais cette propriété n'est pas utilisée.)

Cas d'égalité

Si (x,y) est lié alors x=λy pour un certain scalaire λ et l'on en déduit immédiatement :

Réciproquement, si |<x,y>|=||x|| ||y|| alors le discriminant ci-dessus est nul donc P admet une racine réelle (double) t, et pour ce t on a

donc x=-ty, si bien que (x,y) est lié.

Ou plus directement (avec le t₀ de la variante ci-dessus) : l'hypothèse équivaut à P(t₀)=0 donc à x=-t₀y.

Variante géométrique

Une variante utilise l'identité du théorème de Pythagore.

Un calcul direct permet de voir que les vecteurs et sont orthogonaux. Alors, par le théorème de Pythagore on a :

,

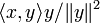
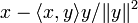
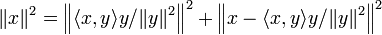
et donc

qui donne l'inégalité souhaitée.

Cette démonstration consiste en fait à calculer la norme du projeté orthogonal du vecteur x sur la droite vectorielle engendrée par y. L'égalité correspond donc au cas où x et y sont linéairement dépendants.

Le cas particulier Rⁿ

Dans l'espace euclidien muni du produit scalaire usuel , où et , une alternative aux démonstrations générales ci-dessus est de déduire l'inégalité (et le cas d'égalité) d'une identité très similaire à celle de la variante géométrique, l'identité de Lagrange, qui s'écrit :

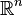
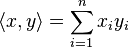
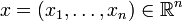
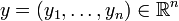
(Pour n=3, une preuve et une interprétation géométrique figurent dans identité de Lagrange dans R³).

Cette identité se démontre de la façon suivante.

Généralisation

L'inégalité seule est vraie dans le contexte un peu plus général d'un semi-produit scalaire (i.e. sans supposer que la forme quadratique associée est définie), en notant encore || || la semi-norme associée :

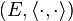
Pour démontrer ce théorème 2, il suffit d'ajouter à la preuve algébrique de l'inégalité du théorème 1 un petit argument dans le cas où ||y||=0.

Cette inégalité fournit le corollaire suivant.

Le corollaire se démontre de la façon suivante.

Pour prouver le sens non immédiat de l'équivalence, supposons que la forme est positive et non dégénérée, et montrons qu'elle est définie. Soit x un vecteur dont la semi-norme est nulle. Le théorème 2 montre que pour tout vecteur y on a , donc, par non dégénérescence, x = 0.