Inégalité d'Azuma - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L’inégalité d'Azuma, parfois appelée inégalité d'Azuma-Hoeffding, est une inégalité de concentration concernant les martingales dont les accroissements sont bornés. C'est une généralisation de l'inégalité de Hoeffding, une inégalité de concentration ne concernant, elle, que les sommes de variables aléatoires indépendantes et bornées.
Énoncé courant
Un des énoncés les plus courants est
Notons que le choix
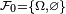
![\scriptstyle\ M_0=\mathbb{E}[M_m].\](https://static.techno-science.net/illustration/Definitions/autres/d/db36a032e0b31d9fa535c7430c2b37b5_0961e7de6fe5d9c30a56f6ecf8d2dcb0.png)
Principe de Maurey
Le principe de Maurey a été énoncé pour la première fois par Maurey dans une note au Compte rendus de l'Académie des Sciences en 1979, et découvert plus tard, semble-t-il indépendamment, par Harry Kesten, en théorie de la percolation. Il est d'usage fréquent en théorie des graphes aléatoires, dans l'analyse des algorithmes randomisés, et en théorie de la percolation. Il est parfois appelé method of bounded differences ou MOBD.
Énoncé
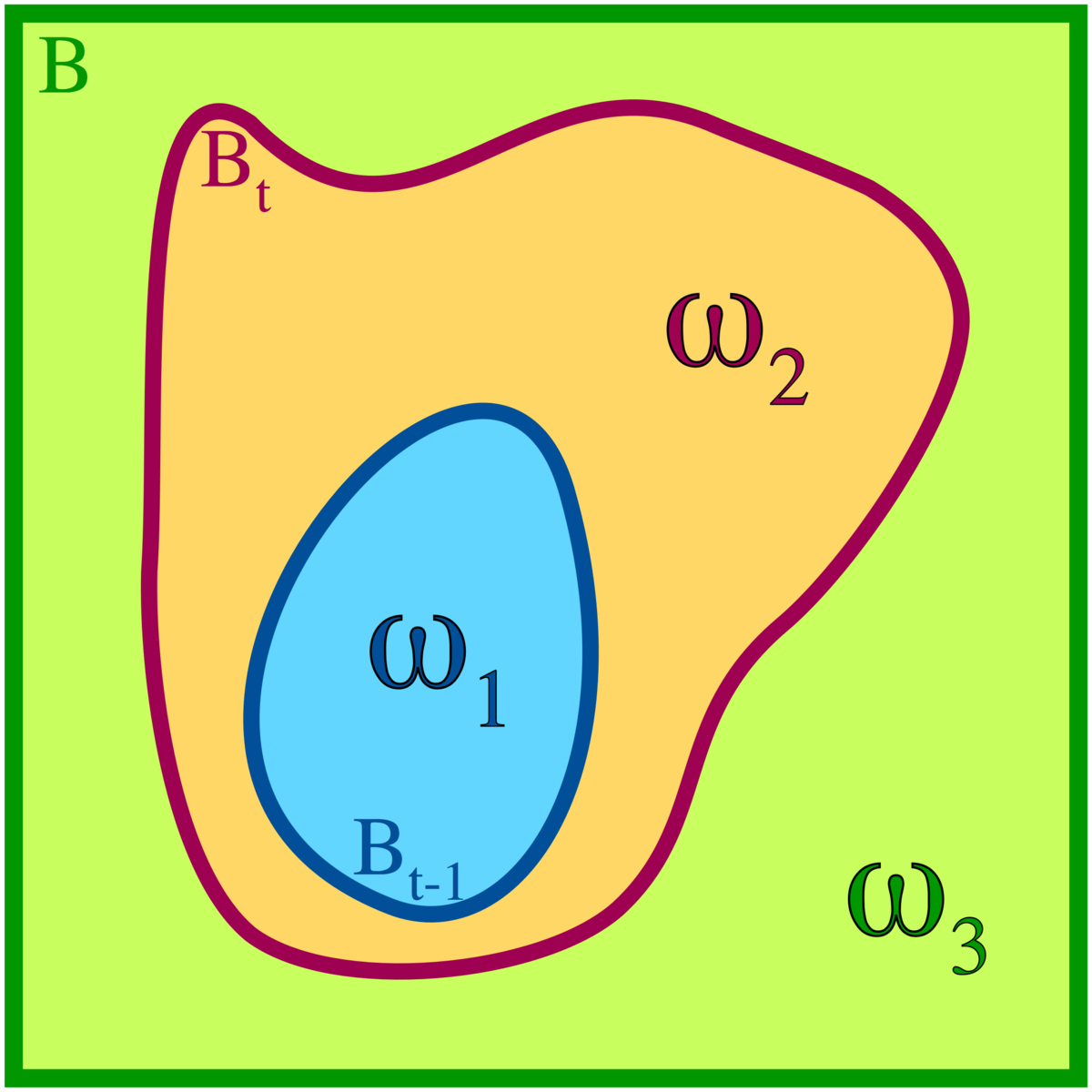
Soit deux ensembles A et B et soit
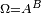
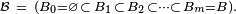
Définition — Une application
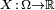
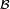
![\scriptstyle\ t\in[\![1,m]\!]\](https://static.techno-science.net/illustration/Definitions/autres/2/2f567e6c690cd8223ffa6f0f57498446_9ece17dc92095f7c09e807c9dd9b5a52.png)
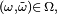
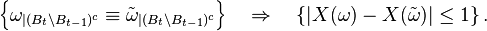
Autrement dit, si les deux applications coincident à l'intérieur de
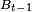
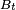
Théorème — On suppose
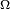
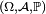
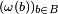
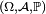
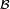

![\begin{align} \mathbb{P}\left(X-\mathbb{E}[X]\ge \lambda\right) &\le\exp\left(-\frac{\lambda^2}{2m}\right), \\ \mathbb{P}\left(X-\mathbb{E}[X]\le -\lambda\right) &\le\exp\left(-\frac{\lambda^2}{2m}\right), \\ \mathbb{P}\left(\left|X-\mathbb{E}[X]\right|\ge \lambda\right) &\le 2\exp\left(-\frac{\lambda^2}{2m}\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/2/2b481e6c381470d2981935671f1be391_5b8f8eb7764f8a8ac51f6d1f773a2de5.png)
On considère la filtration filtration
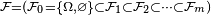
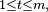
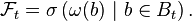
Pour
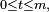
![M_t=\mathbb{E}\left[X\left|\ \mathcal{F}_t\right.\right].](https://static.techno-science.net/illustration/Definitions/autres/f/fc578cfc56bb2c9ed206df257be9cde3_2bbc7da810281424ef194a5153080eb5.png)
Ainsi
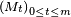
![\scriptstyle\ M_0=\mathbb{E}\left[X\right],\](https://static.techno-science.net/illustration/Definitions/autres/2/2421dd55b850aa3b6befadf4d594a74c_ee28f8f1c74c73a9cd4c54da5bd13a13.png)
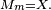
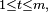
-
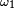

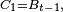
-
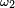

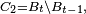
-
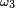

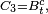
Comme les
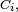
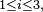

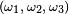
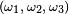
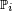
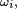
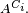
 &=\int_{A^{C_{3}}} X(\omega_{1},\,\omega_{2},\, w_{3}) \mathbb{P}_{3}(dw_{3}), \\ &=\int_{A^{C_{3}}} \left(\int_{A^{C_{2}}} X(\omega_{1},\,\omega_{2},\, w_{3}) \mathbb{P}_{2}(dw_{2})\right)\mathbb{P}_{3}(dw_{3}). \\ \mathbb{E}\left[X\left|\ \mathcal{F}_{t-1}\right.\right](\omega) &=\int_{A^{C_{3}}} \left(\int_{A^{C_{2}}} X(\omega_{1},\,w_{2},\, w_{3}) \mathbb{P}_{2}(dw_{2})\right)\mathbb{P}_{3}(dw_{3}). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/2/2a24f05ad888dca0fe164ab38dd6bfd0_609d984d7162713e25e0f7e22ec58cd8.png)
Ainsi
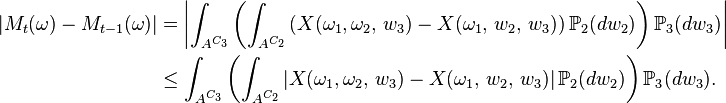
Mais les deux triplets
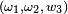
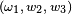
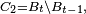
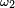
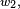
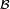
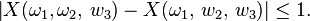
Par conséquent
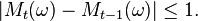
Application à un modèle d'urnes et de boules
Dans cet exemple, l'intérêt d'une inégalité de concentration précise est de justifier une méthode statistique de comptage approximatif pouvant servir, par exemple, à déceler une attaque de virus informatique.
Une inégalité de concentration
On jette m boules au hasard dans n boites, expérience probabiliste dont un évènement élémentaire

![\scriptstyle\ B=[\![1,m]\!]\](https://static.techno-science.net/illustration/Definitions/autres/3/3bbdbc9ab812fd257b164b0b5d996c02_e94a218bd83889e5ae36f0519c59b024.png)
![\scriptstyle\ A=[\![1,n]\!]\](https://static.techno-science.net/illustration/Definitions/autres/3/351886763a033dd38fdbb2c605514366_fd2f502f3ca322a9b12af5929153848f.png)
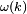
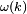

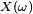
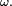
![\mathbb{E}[X]\ =\ n\left(1-\tfrac1n\right)^m.](https://static.techno-science.net/illustration/Definitions/autres/1/1b7a3a982df32578e3839520743a057e_c520942ed342413f45d995e3072501a5.png)
Pour le choix
![\scriptstyle\ B_{t}=[\![1,t]\!],\](https://static.techno-science.net/illustration/Definitions/autres/0/0d9aa773c2dc4db7648a48f92d333384_de788cd7b31496d03aadede49f8c4038.png)
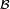
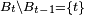
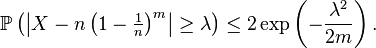
Une inégalité plus précise est obtenue en appliquant la de l'inégalité d'Azuma.
Un problème de comptage approché
Il s'agit d'estimer le nombre m d'utilisateurs différents, identifiés, à un noeud du réseau, par l'entête du paquet de données qu'ils envoient. L'idée est qu'une attaque de virus ne se traduit pas par une augmentation décelable du volume du trafic (le gros du volume étant fourni, par exemple, par des téléchargements de fichiers, lesquels sont scindés en nombreux paquets qui ont tous la même entête, caractérisant le même utilisateur), mais par une augmentation drastique du nombre d'utilisateurs différents, à cause d'un envoi massif et concerté de mails (tous de petit volume, comparés à des téléchargements).
Chaque fois qu'un paquet de données est reçu à un noeud du réseau, l'utilisateur b émetteur du paquet est reconnu à l'aide de l'entête
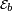
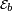
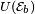
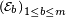
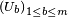
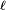
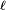
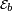
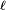
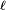
On reçoit un grand nombre (P) de paquets en un laps de temps très court. On dispose seulement de n cases mémoires et on veut compter le nombre m d'utilisateurs différents émetteurs de ces paquets. Par manque de place mémoire, il est impossible de stocker au fur et à mesure les entêtes des paquets déjà reçus, et par manque de temps il serait impossible de tester si une nouvelle entête reçue fait partie de la liste des entêtes déjà récoltées. Un calcul exact de m est donc impossible. On se donne alors n cases, numérotées de 1 à n, considérées comme libres, ou bien occupées. Au départ toutes les cases sont considérées comme libres. A chaque paquet reçu, l'entête correspondante est hachée, produisant un nombre U aléatoire uniforme sur [0,1], et la case n°
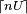
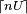
Ainsi l'état de l'ensemble des n cases après réception des P paquets ne dépend pas du volume P du trafic, mais uniquement de la suite des m entêtes hashées
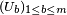
![\scriptstyle\ \mathbb{E}[X]\](https://static.techno-science.net/illustration/Definitions/autres/b/b007f12b3f096ca95412a411062e9a2f_8bd4d7b82606027ef254327c75b83501.png)
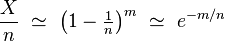
est assez précise pour permettre de reconstituer le ratio r=m/n, et, partant de là, le nombre m d'utilisateurs différents, inconnu jusque là, en fonction de X et de n, qui sont connus : on choisit comme approximation de r le nombre
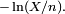
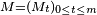
![\forall t\in[\![1,m]\!],\qquad \mathbb{P}(|M_t-M_{t-1}|\le 1)=1.](https://static.techno-science.net/illustration/Definitions/autres/9/9191734c1ae2142a03dfa6f61cedb763_e4874a04354e291c130a870d82af4d36.png)
![\begin{align} \mathbb{P}\left(M_m-\mathbb{E}[M_m]\ge \lambda\right) &\le\exp\left(-\frac{\lambda^2}{2m}\right), \\ \mathbb{P}\left(M_m-\mathbb{E}[M_m]\le -\lambda\right) &\le\exp\left(-\frac{\lambda^2}{2m}\right), \\ \mathbb{P}\left(\left|M_m-\mathbb{E}[M_m]\right|\ge \lambda\right) &\le 2\exp\left(-\frac{\lambda^2}{2m}\right). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/9/968f1a09c3dcf12fd575c63e54702942_2b90bf1664e264dc767f614403318d8c.png)