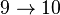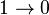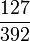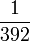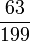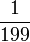Indices de pouvoir - Définition
La liste des auteurs de cet article est disponible ici.
Interprétation probabiliste des indices de pouvoirs
L'intuition d'Owen et Straffin repose sur l'idée que l'ordre de Shapley-Shubick est inadapté car il ne fonctionne pas dans la réalité.
Idée:
Repose sur la probabilité d'être pivôt. Le problème est de montrer qu'il s'agit d'une probabilité. C'est pourquoi Straffin a créé un vecteur d'acceptabilité (P1,...,Pn) avec Pi: la probabilité que i dise oui
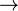
- Indépendance : chaque Pi est choisit indépendant dans une uniforme [0,1].
- Homogénéité : on tire un chiffre au hasard entre 0 et 1, P et tout le monde à la même.
On note αi la probabilité que l'individu i soit pivôt.
Proposition: La probabilité αi est égale à Bi, pouvoir de Banzhaf, sous l'hypothèse d'indépendance et à SSI, pouvoir de Shapley-Shubik, sous l'hypothèse d'homogénéité.
La démonstration de cette proposition repose sur le calcul de la probabilité que tous les individu sauf i qui se trouvent dans une coalition gagnante et votent oui, les autres non, et que l'individu i soit pivôt (hors coalition).
Postulats et paradoxes
Paradoxe de la monotonie
Soit (N,v) un jeu de vote avec un quota q et une distribution de pouvoirs (w1,...,wn). L'indice α est sujet au paradoxe de la monotonie si il existe deux joueurs i et j tels que:
- wi > wj et αi(v) < αj(v)
Exemple n°6: HP dans le tableau n°8
Paradoxe du transfert
Soit (N,v) un jeu de vote avec un quota q et une distribution de pouvoirs (w1,...,wn) et (N',v') un jeu de vote avec un quota q et une distribution de pouvoirs (w1',...,wn') tels que:
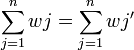
Supposons qu'il existe i vérifiant pour tout
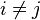
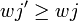
L'indice α est sujet au paradoxe du transfert si :αi(v') > αi(v).
Exemple n°7: Soit les jeux [8;5,3,1,1,1] et [8;4,4,1,1,1]. Ils ne diffèrent que par la différence de poids entre les deux premiers joueurs: dans le premier jeu le joueur n°1 a un poids de 5 et le joueur n°2 un poids de 3, alors que dans le second jeu les deux joueurs ont un poids de 4.
Les deux tableaux suivants donnent les résultats des combinaisons gagnantes des jeux:
Tableau n°9: Les coalitions minimales gagnantes du premier jeu
| Coalitions minimales gagnantes | 1 | 2 | 3 | 4 | 5 | d(S) | s |
|---|---|---|---|---|---|---|---|
| 1,2 | 1 | 1 | 0 | 0 | 0 | 2 | 2 |
| 1,3,4,5 | 1 | 0 | 1 | 1 | 1 | 4 | 4 |
Tableau n°10: Les coalitions minimales gagnantes du second jeu
| Coalitions minimales gagnantes | 1 | 2 | 3 | 4 | 5 | d(S) | s |
|---|---|---|---|---|---|---|---|
| 1,2 | 1 | 1 | 0 | 0 | 0 | 2 | 2 |
Avec l'indice de Deegan-Packel on obtient les résultats suivants:
Tableau n°11: Les résultats pour l'indice de Deegan-Packel des deux jeux
| Joueur | Jeux n°1 | Jeux n°2 |
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
| 0 |
| 4 |
| 0 |
| 5 |
| 0 |
Paradoxe du bloc
Soit (N,v) un jeu de vote avec un quota q et une distribution de pouvoirs (w1,...,wn) et ((N\j),v') un nouveau jeu de vote le même quota q et une distribution de poids (w1',..., wj − 1', wj + 1',...,wn') tels que pour tout
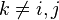
L'indice α est sujet au paradoxe du bloc si :αj(v) > 0 et α'i(v') < αi(v).
Exemple n°8: Soit les jeux [25;9,9,7,1,1,1,1,1,1,1] et [25;10,9,7,1,1,1,1,1,1]. Ils ne diffèrent que le transfert du poids du dernier joueur du jeux n°1 sur celui du premier joueur du jeux n°2:
On passe donc d'un jeu à dix joueurs à un jeu à neuf joueurs.
On peut aussi regrouper les joueurs ayant même poids.
On a donc pour le jeu n°1:
- J1
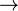
- J2
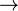
- J3
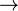
On a donc pour le jeu n°2:
- J1
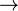
- J2
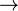
- J3
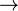
- J4
On observe ce paradoxe avec l'indice de Banzhaf dans les tableaux suivant:
Tableau n°12: Les résultats pour le jeu n°1
| Indice | A | B | C |
|---|---|---|---|
| Banzhaf | 0,329 |
|
|
Tableau n°13: Les résultats pour le jeu n°2
| Indice | A | B | C | D |
|---|---|---|---|---|
| Banzhaf | 0,327 | 0,327 |
|
|
Remarque n°5: Alors qu'on a augmenté son poids de 1, le premier joueur a non seulement le même pouvoir que le second joueur, qui lui a un poids de 9, mais en plus il a perdu du pouvoir par rapport à la configuration antérieur.
Tableau résumant les paradoxes
Tableau n°14: Les paradoxes en fonction des indices
| Indices | Bloc | Monotone | Transfert |
|---|---|---|---|
| Shapley-Shubik | oui | oui | oui |
| Banzhaf non normalisé | oui | oui | oui |
| Banzhaf | non | oui | non |
| Johnston | non | oui | non |
| Deegan-Packel | non | non | non |
| Hollard-Packel | non | non | non |