Indices de pouvoir - Définition
La liste des auteurs de cet article est disponible ici.
Définitions, exemples et notations
L'étude du pouvoir de vote a été réalisée, pour la majeure partie, en se fondant sur la théorie des jeux coopératifs. Ce sont donc les notions et les outils de ce théorie qu'utilisent les indices de pouvoir. Le but de cette partie est de d'expliquer les notations employées et présenter les éléments de théorie des jeux qui seront utiles.
Définition d'un jeu de vote
Un jeu de vote (ou jeu de contrôle) est un couple (N,v) où N={1,...,i,...,n} représente l'ensemble des "joueurs" (ici les votants) et v une valeur appartenant à {0,1} telle qu'à chaque groupe d'individus on associe à chaque fois un nombre.
Définition d'une coalition gagnante
Une coalition S est dite gagnante si v(S)=1 et perdante si v(S)=0. On note s le nombre de joueurs dans S, Gi(v) l'ensemble des coalitions gagnantes et Gi(v) l'ensemble des coalitions gagnantes contenant le joueur i.
Remarque n°1: Si l'on considère l'ensemble des joueurs comme un ensemble d'individus prenant part à un processus de décision collective, on peut généralement modéliser ce processus par un jeu de vote. Un coalition gagnante est alors définie comme un ensemble de votants tels que s'ils votent à l'unanimité pour une proposition, celle-ci est adoptée. On peut définir cette coalition comme une majorité généralisée.
Remarque n°2: La valeur v indique alors le statut de chaque coalition et par conséquent autorise la formalisation du processus de décision collective. Dans cette configuration l'abstention est exclue: devant une proposition, le joueur n'a le choix de voter qu'entre "oui" et "non".
Définition d'un joueur décisif
Un individu i est dit décisif pour une coalition gagnante S si le retrait de ce participant rend la coalition S perdante, c'est-à-dire si v(S) = 1 et v(S\{i})=0. On note d(S) le nombre de joueurs décisifs dans la coalition S, Di(v) l'ensemble des coalitions pour lesquelles le joueur i est décisif.
Définition d'une coalition minimale gagnante
Une coalition est dite minimale gagnante si c'est une coalition gagnante dont tous les joueurs sont décisifs. On note M(v) l'ensemble des coalitions gagnantes de taille minimale (c'est-à-dire où chaque individu est décisif) et Mi(v) l'ensemble des coalitions gagnantes de taille minimale auquel le joueuri appartient.
Définition d'un jeu monotone
Un jeux de vote remplissant la condition suivante:
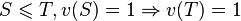
est alors dit monotone.
Définition d'un jeu pondéré
Un jeux simple est dit pondéré si il existe un quota q et un poids wi > 0 pour chaque joueur tel que:
- v(S) = 1 si
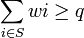
- 0 sinon
Le jeux se note [q; w1,...,wn]
Exemple n°1
Le jeu de vote pour la Communauté Européenne en 1952 s'écrit:
Définition d'un jeu propre
Un jeux simple est supposé propre si pour une coalition gagnante, le complémentaire de celle-ci est perdant:
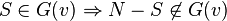
Définition d'un jeu fort
Un jeux simple est supposé fort si:
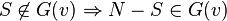
Remarque: Cette condition est plus contraignante que celle de la définition n°7. En effet un jeu pondéré est propre si q > w / 2, avec:
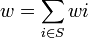
Si l'on suppose w impaire, un jeu pondéré est fort si q = (w + 1) / 2.
Exemple n°2
Voici un jeux important à quatre joueurs, où les calculs sont élémentaires, qui sert de référence:
On a un quota de 3 et le jeux suivant: [3;2,1,1,1].
On a quatre individus a, b, c et d, où a dispose d'un poids de 2 et les trois autres d'un poids de 1.
On peut écrire les coalitions gagnantes dans le tableau suivant:
Tableau n°1
| Coalitions gagnantes | a | b | c | d | d(S) = nombre de joueurs décisifs | s = taille de la coalition |
|---|---|---|---|---|---|---|
| a,b | 1 | 1 | 0 | 0 | 2 | 2 |
| a,c | 1 | 0 | 1 | 0 | 2 | 2 |
| a,d | 1 | 0 | 0 | 1 | 2 | 2 |
| a,b,c | 1 | 0 | 0 | 0 | 1 | 3 |
| a,b,d | 1 | 0 | 0 | 0 | 1 | 3 |
| a,c,d | 1 | 0 | 0 | 0 | 1 | 3 |
| b,c,d | 0 | 1 | 1 | 1 | 3 | 3 |
| a,b,c,d | 0 | 0 | 0 | 0 | 0 | 4 |
On peut ensuite écrire le tableau des coalitions minimales gagnantes:
Tableau n°2
| Coalitions gagnantes | a | b | c | d | d(S) = nombre de joueurs décisifs | s = taille de la coalition |
|---|---|---|---|---|---|---|
| a,b | 1 | 1 | 0 | 0 | 2 | 2 |
| a,c | 1 | 0 | 1 | 0 | 2 | 2 |
| a,d | 1 | 0 | 0 | 1 | 2 | 2 |
| b,c,d | 0 | 1 | 1 | 1 | 3 | 3 |

















































