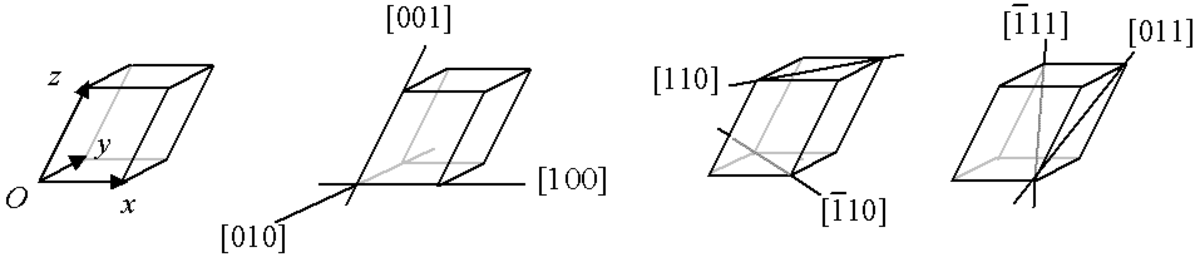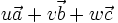Indices de Miller et indices de direction - Définition
La liste des auteurs de cet article est disponible ici.
Repérage d'une direction
Une direction peut se représenter par un vecteur. On choisit pour cela un vecteur ayant des coordonnées entières : une direction contient au moins deux motifs pour que l'on puisse définir sa densité, et les motifs sont décalés d'une combinaison linéaire entière des vecteurs de la base. Cette direction est notée [uvw] où u, v et w sont les coordonnées entières. Les nombres négatifs sont notés avec un trait au-dessus (u se lit « moins u ») :
- [111] (ou le vecteur opposé [111]) désigne la grande diagonale de la maille ;
- [111] (ou l'opposé [111]) et [111] (ou l'opposé [111]) désignent les deux autres diagonales ;
- [100], [010] et [001] désignent les vecteurs de la base.
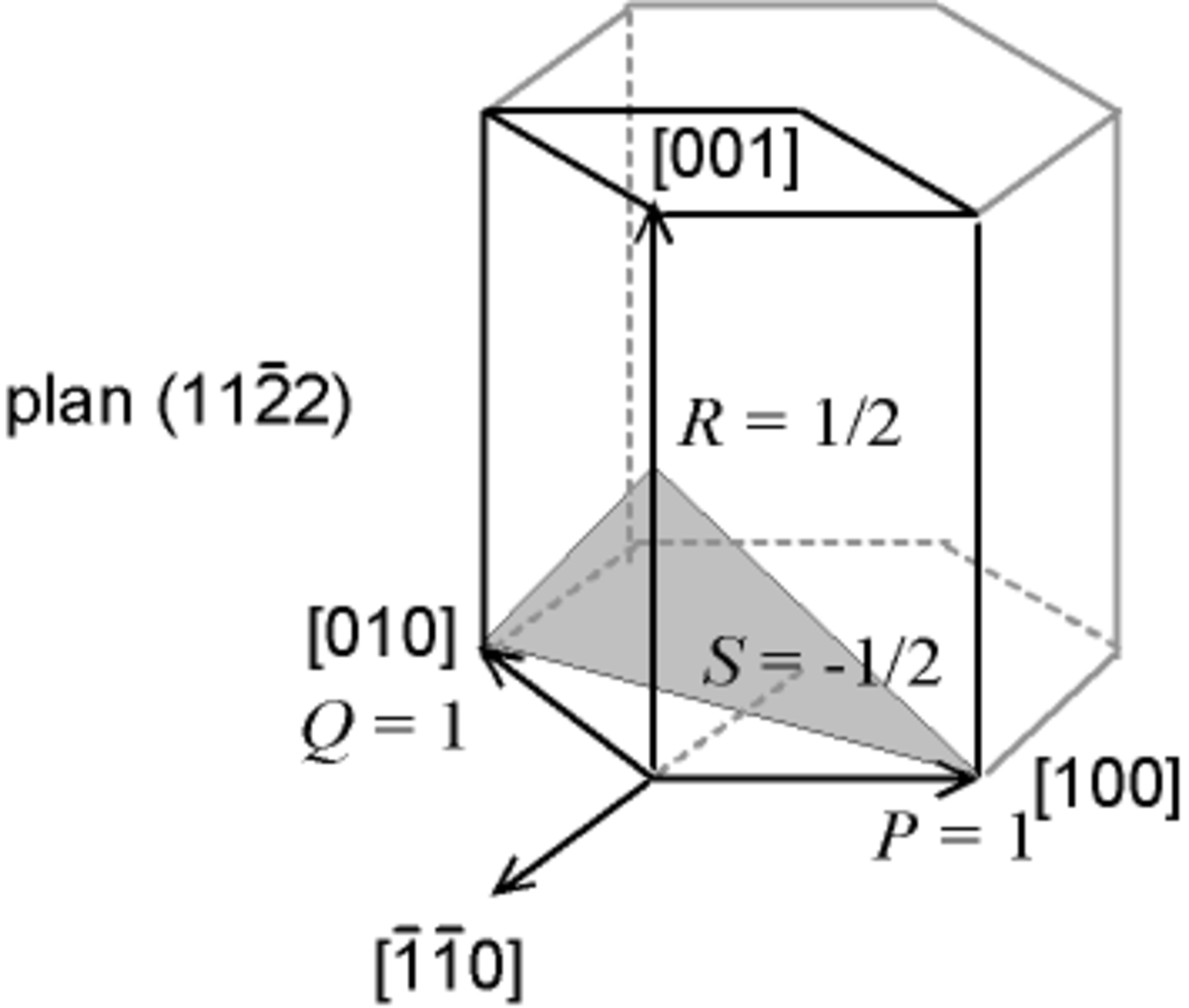
Si l'on note
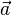
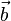
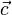
u, v et w sont des coordonnées de type contravariantes.
- Note
- Dans le cas général, la base
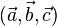
Indexation des pics de diffraction
- Note
- Par « pic », nous désignons non seulement les pics des diffractogrammes dans le cas des enregistrements numériques, mais aussi les taches de diffraction dans le cas de la diffraction sur un monocristal (cliché de Laue, microscopie électronique en transmission), ainsi que les anneaux de diffraction dans le cas de la diffraction sur une poudre (chambre de Debye-Scherrer).
- Voir l'article Théorie de la diffraction sur un cristal.
Dans les expériences de diffraction avec une longueur d'onde de l'ordre des paramètres de maille (diffraction de rayons X, diffraction de neutrons, diffraction d'électrons en microscopie électronique en transmission), la position des pics de diffraction peut se calculer en fonction des distances interréticulaires, par la loi de Bragg.
On peut ainsi relier chaque pic à un plan (hkl ) ; les indices de miller du plan sont les indices du pic.
Symétries cristallines et permutation des indices
Certaines structures cristallines possèdent des symétrie particulières permettant la permutation des indices.
Cristal à symétrie cubique
Pour un cristal suivant un réseau de Bravais cubique, les trois diagonales sont équivalentes, les trois faces du cube sont équivalentes, … ; on peut donc permuter à volonté les indices et prendre les opposés d'un ou de plusieurs indices, cela représentera immuablement une direction ayant les mêmes propriétés.
L'ensemble des directions obtenues par permutation est appelées « famille de direction », et est notée entre crochet :
- <uvw> désigne à la fois [uvw], [uwv], [vuw], [vwu], [wuv], [wvu] ainsi que les combinaisons obtenues en changeant un ou deux signes.
Par exemple
- <100> désigne les directions [100], [100], [010], [010], [001] et [001] ;
- <110> désigne les directions [110], [110], [110], [101], [101], [101], [011], [011] et [011] (ainsi que leurs opposé).
Il en est de même pour les plans, on peut permuter les indices de Miller. Une famille de plans est alors notée entre accolades :
- {hkl} désigne les plans (hkl), (hlk), (khl), (klh), (lhk), (lkh) ainsi que les combinaisons obtenues en changeant un ou deux signes.
Cristal à symétrie hexagonale
Dans le cas des structures à symétrie hexagonale, ou trigonale, on définit parfois un quatrième indice pour désigner les plans, (hkil ) ; c'est la notation de Bravais-Miller. L'indice i, placé en troisième position, est redondant (les trois indices h, k et l suffisent à eux seuls à définir un plan) ; il est défini par
- i = -h - k
Cette notation permet d'appliquer des permutations circulaires d'indice pour définir des familles de plans.
En fait, si l'on considère le plan de base (001), ce plan a une symétrie d'ordre 3, c'est-à-dire qu'il est invariant par une rotation d'1/3 de tour (2π/3 rad, 120 °). Il contient donc trois directions identiques [100], [010] et [110]. Si l'on prend l'intersection du plan avec ces trois axes, l'inverse des abscisses des intersections donnent les indices h, k et i.