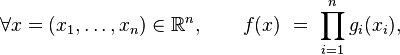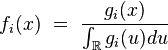Indépendance (probabilités) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Indépendance de deux évènements - Indépendance des variables aléatoires - Indépendance de n évènements - Lemme de regroupement - Indépendance des tribus - Indépendance et information

Introduction

L'indépendance est une notion probabiliste qualifiant de manière intuitive des événements aléatoires n'ayant aucune influence l'un sur l'autre. Il s'agit d'une notion très importante en statistique et calcul de probabilités.

Par exemple, la valeur d'un premier lancer de dés n'a aucune influence sur la valeur du second lancer. De même, pour un lancer, le fait d'obtenir une valeur inférieure ou égale à quatre n'influe en rien sur la probabilité que le résultat soit pair ou impair : les deux événements sont dits indépendants.

L'indépendance ou non de deux événements n'est pas toujours facile à établir.

Indépendance de deux évènements

La définition mathématique de l'indépendance de deux évènements est la suivante :

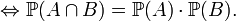
Définition — A et B sont indépendants $\Leftrightarrow \mathbb{P}(A \cap B) = \mathbb{P}(A) \cdot \mathbb{P}(B).$

La définition mathématique ci-dessus est assez peu parlante. Le lien entre le concept intuitif d'indépendance et la "formule produit" ci-dessus apparaît plus clairement si l'on introduit la notion de probabilité conditionnelle :

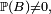
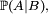
Définition — Si $\scriptstyle\ \mathbb{P}(B) \neq 0,$ la probabilité conditionnelle de A sachant B, notée $\scriptstyle\ \mathbb{P}(A\mid B),\$ est définie par la relation ci-dessous :

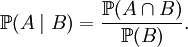
$\mathbb{P}(A\mid B)={\mathbb{P}(A \cap B) \over \mathbb{P}(B)}.$

En excluant les cas particuliers peu intéressants où B est impossible, et où B est certain, on peut alors reformuler la définition de l'indépendance de la manière suivante

Définition — Lorsque la probabilité de B n'est ni nulle, ni égale à 1, A et B sont indépendants si l'une des conditions suivantes, toutes équivalentes, est remplie :

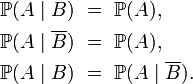
$\begin{align}\mathbb{P}(A\mid B)\ &=\ \mathbb{P}(A),\\\mathbb{P}(A\mid \overline{B})\ &=\ \mathbb{P}(A),\\\mathbb{P}(A\mid B)\ &=\ \mathbb{P}(A\mid \overline{B}).\end{align}$

Ainsi les évènements A et B sont dits indépendants si notre pronostic sur l'évènement A est le même :

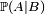
si on sait que l'évènement B s'est produit (pronostic $\scriptstyle\ \mathbb{P}(A\mid B)\$ ),
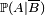
si on sait que l'évènement B ne s'est pas produit (pronostic $\scriptstyle\ \mathbb{P}(A\mid \overline{B})\$ ),
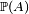
si on ne sait rien sur le statut de l'évènement B (pronostic $\scriptstyle\ \mathbb{P}(A)\$ ).

Autrement dit, A est dit indépendant de B si notre pronostic sur l'évènement A n'est affecté par aucune information concernant B, ni par l'absence d'information concernant B. On peut échanger les rôles de A et de B dans la définition utilisant les probabilités conditionnelles, à condition bien sûr d'exclure les cas particuliers peu intéressants où A est impossible, et où A est certain.

Bien que la définition utilisant les probabilités conditionnelles soit plus intuitive, elle a l'inconvénient d'être moins générale, et de ne pas faire jouer un rôle symétrique aux deux événements A et B.

Notons par ailleurs qu'un évènement certain A est indépendant de tout évènement B quel qu'il soit. Un évènement impossible est également indépendant de tout autre évènement. En particulier, un événement A est indépendant de lui-même à la condition que A soit soit certain, soit impossible. En effet, si l'événement A est indépendant de lui-même, on peut écrire :

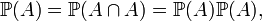
$\mathbb{P}(A) = \mathbb{P}(A \cap A) = \mathbb{P}(A)\mathbb{P}(A),\,$

et on en déduit que la probabilité de l'événement A vaut soit 0, soit 1.

Indépendance des variables aléatoires

Définitions

Il y a plusieurs définitions équivalentes de l'indépendance d'une famille finie de variables aléatoires. On peut en particulier définir l'indépendance d'une famille de tribus, et voir ensuite l'indépendance des évènements et l'indépendance des variables aléatoires comme des cas particuliers de l'indépendance des tribus. Cela permet de démontrer certains résultats généraux sur l'indépendance une seule fois, pour les tribus, puis d'en déduire la version "évènements" et la version "variables aléatoires" de ce résultat général immédiatement (un exemple est le lemme de regroupement). Cependant, il est peut-être préférable de donner d'abord deux définitions de l'indépendance des variables aléatoires qui soient opératoires pour les applications, et quelques critères commodes. 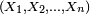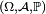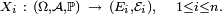Dans ce qui suit on considère une suite $\scriptstyle\ (X_1, X_2, \dots,X_n)$ de variables aléatoires définies sur le même espace de probabilité $\scriptstyle\ (\Omega, \mathcal{A}, \mathbb{P})$ , mais éventuellement à valeurs dans des espaces différents : $\scriptstyle\ X_i\ :\ (\Omega, \mathcal{A}, \mathbb{P})\ \rightarrow\ (E_i,\mathcal{E}_i),\quad 1\le i\le n.$

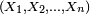
Définition — $\scriptstyle\ (X_1, X_2, \dots,X_n)$ est une famille de variables aléatoires indépendantes si l'une des deux conditions suivantes est remplie :

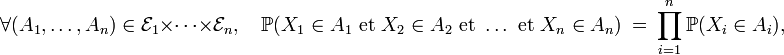
$\forall (A_1,\dots,A_n)\in\mathcal{E}_1\times\dots\times\mathcal{E}_n,\quad\mathbb{P}(X_1\in A_1\text{ et }X_2\in A_2\text{ et }\dots\text{ et }X_n\in A_n)\ =\ \prod_{i=1}^n\mathbb{P}(X_i\in A_i),$
on a l'égalité

$\mathbb{E}\left[\prod_{i=1}^n\ \varphi_i(X_i)\right]\ =\ \prod_{i=1}^n\mathbb{E}\left[\varphi_i(X_i)\right],$

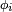
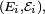
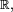
pour n'importe quelle suite de fonctions $\scriptstyle\ \phi_i$ définies sur $\scriptstyle\ (E_i,\mathcal{E}_i),$ à valeurs dans $\scriptstyle\ \R,\$ dès que les espérances ci-dessus ont un sens.

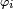
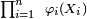
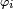
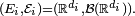
Les espérances ci-dessus ont un sens si les $\scriptstyle\ \varphi_i\$ sont mesurables, et si $\scriptstyle\ \prod_{i=1}^n\ \varphi_i(X_i)\$ est intégrable, ou si les $\scriptstyle\ \varphi_i\$ sont positives ou nulles. Typiquement, dans les applications, $\scriptstyle\ (E_i,\mathcal{E}_i)=(\mathbb{R}^{d_i},\mathcal{B}(\mathbb{R}^{d_i})).$ Dans le cas de deux variables aléatoires réelles cela donne :

Définition — Deux variables aléatoires réelles X et Y sont indépendantes si l'une des deux conditions suivantes est remplie :

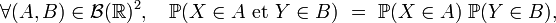
$\forall (A,B)\in\mathcal{B}(\mathbb{R})^{2},\quad\mathbb{P}(X\in A\text{ et }Y\in B)\ =\ \mathbb{P}(X\in A)\ \mathbb{P}(Y\in B),$
on a

$\mathbb{E}\left[g(X)\cdot h(Y)\right] = \mathbb{E}[g(X)]\cdot \mathbb{E}[h(Y)]$

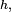
pour tout couple de fonctions boréliennes $\scriptstyle\ g$ et $\scriptstyle\ h,\$ dès que les espérances ci-dessus ont un sens.

Les définitions précédentes traitent de familles finies de variables aléatoires, numérotées de 1 à n par commodité, sans que cela restreigne la généralité des énoncés : en effet, on peut toujours numéroter de 1 à n les éléments d'une famille finie de variables aléatoires. De plus, les définitions font jouer des rôles symétriques à chaque élément de la famille, si bien que le choix d'une numérotation ou d'une autre est sans effet sur la vérification de la définition.

L'indépendance d'une famille quelconque (éventuellement infinie) de variables aléatoires est la suivante :

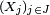
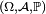
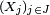
Définition — Une famille quelconque $\scriptstyle\ (X_{j})_{j\in J}\$ de variables aléatoires définies sur $\scriptstyle\ (\Omega,\mathcal{A},\mathbb{P})\$ est une famille de variables aléatoires indépendantes si et seulement si toute sous famille finie de $\scriptstyle\ (X_{j})_{j\in J}\$ est une famille de variables aléatoires indépendantes (c'est-à dire, si et seulement si, pour toute partie finie I de J, $\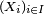scriptstyle\ (X_{i})_{i\in I}\$ est une famille de variables aléatoires indépendantes).

Cas des variables aléatoires à densité

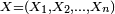
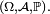
Soit une suite $\scriptstyle\ X=(X_1, X_2, \dots,X_n)$ de variables aléatoires réelles définies sur le même espace de probabilité $\scriptstyle\ (\Omega, \mathcal{A}, \mathbb{P}).\$

Théorème —

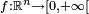
Si $\scriptstyle\ X\$ possède une densité de probabilité $\scriptstyle\ f:\R^n\rightarrow [0,+\infty[\$ qui s'écrit sous forme "produit" :

$\forall x=(x_1,\dots,x_n)\in\R^n,\qquad f(x)\ =\ \prod_{i=1}^ng_i(x_i),$

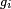
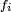
où les fonctions $\scriptstyle\ g_i\$ sont boréliennes et positives ou nulles, alors $\scriptstyle\ X\$ est une suite de variables indépendantes. De plus, la fonction $\scriptstyle\ f_i\$ définie par

$f_i(x)\ =\ \frac{g_i(x)}{\int_{\R}g_i(u)du}$

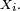
est une densité de probabilité de la variable aléatoire $\scriptstyle\ X_i.\$

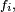
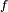
Réciproquement, si $\scriptstyle\ X\$ est une suite de variables aléatoires réelles indépendantes de densités de probabilité respectives $\scriptstyle\ f_i,\$ alors $\scriptstyle\ X\$ possède une densité de probabilité, et la fonction $\scriptstyle\ f\$ définie par

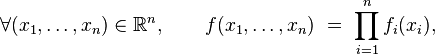
$\forall (x_1,\dots,x_n)\in\R^n,\qquad f(x_1,\dots,x_n)\ =\ \prod_{i=1}^nf_i(x_i),$

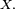
est une densité de probabilité de $\scriptstyle\ X.\$

Sens direct.

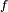
Comme la densité $\scriptstyle\ f\$ est sous forme produit, on a

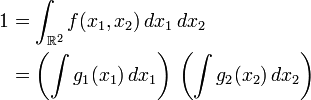
$\begin{align} 1 &= \int_{\R^2}f(x_1,x_2) \, dx_1 \, dx_2\\ &=\left(\int g_1(x_1)\, dx_1\right) \, \left(\int g_2(x_2) \, dx_2\right) \end{align}$

et par suite

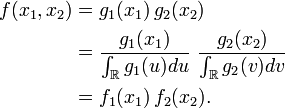
$\begin{align} f(x_1,x_2) &= g_1(x_1)\, g_2(x_2) \\ &= \frac{g_1(x_{1})}{\int_{\R}g_1(u)du}\ \frac{g_2(x_{2})}{\int_{\R}g_2(v)dv}\\ &= f_1(x_1) \,f_{2}(x_2). \end{align}$

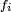
Par construction les fonctions $\scriptstyle\ f_i\$ sont d'intégrale 1, donc

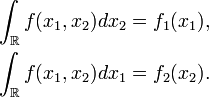
$\begin{align} \int_{\R} f(x_1,x_2) dx_2 &= f_1(x_1), \\ \int_{\R} f(x_1,x_2) dx_1 &= f_2(x_2). \end{align}$

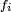
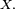
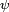
Ainsi les fonctions $\scriptstyle\ f_i\$ sont les densités de probabilités marginales des deux composantes de $\scriptstyle\ X.\$ Par suite, pour tout couple de fonctions $\scriptstyle\ \varphi\$ et $\scriptstyle\ \psi\$ tel que le premier terme ci-dessous ait un sens, on a

$\begin{align} \operatorname{E}[\varphi(X_1)\psi(X_2)] &= \int \int \varphi(x_1)\psi(x_2)f(x_1,x_2) \, dx_1 \, dx_2\\ &= \int \int \varphi(x_1)f_1(x_1)\psi(x_2)f_2(x_2) \, dx_1 \, dx_2\\ &= \int \varphi(x_1)f_1(x_1) \, dx_1 \int \psi(x_2)f_{2}(x_2) \, dx_2\\ &= \operatorname{E}[\varphi(X_1)] \operatorname{E}[\psi(X_2)]\end{align}$

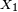
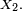
ce qui entraine l'indépendance des variables $\scriptstyle\ X_{1}\$ et $\scriptstyle\ X_{2}.\$

Sens réciproque. Il suffit de montrer que

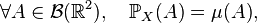
$\forall A\in \mathcal{B}(\R^2),\quad \mathbb{P}_{X}(A)=\mu(A),$

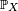
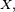
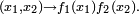
où $\scriptstyle\ \mathbb{P}_{X}\$ est la loi de $\scriptstyle\ X,\$ et où $\scriptstyle\ \mu\$ est la mesure ayant pour densité $\scriptstyle\ (x_1,x_2)\rightarrow f_1(x_1)f_{2}(x_2).\$ Or

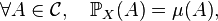
$\forall A\in \mathcal{C},\quad \mathbb{P}_{X}(A)=\mu(A),$

où $\scriptstyle\ \mathcal{C}\$ est la classe des pavés boréliens :

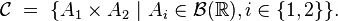
$\mathcal{C}\ =\ \{A_1\times A_2\ |\ A_i\in\mathcal{B}(\R),i\in\{1,2\}\}.$

En effet

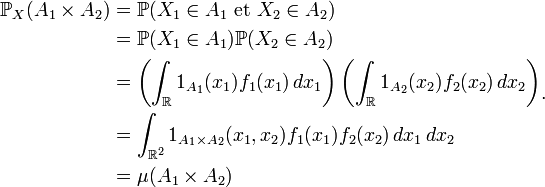
$\begin{align} \mathbb{P}_{X}(A_1\times A_2) &= \mathbb{P}(X_1\in A_1\text{ et }X_2\in A_2)\\ &= \mathbb{P}(X_1\in A_1)\mathbb{P}(X_2\in A_2)\\ &= \left(\int_{\R} 1_{A_1}(x_1)f_1(x_1) \, dx_1\right)\left(\int_{\R} 1_{A_2}(x_2)f_2(x_2) \, dx_2\right)\\ &= \int_{\R^2} 1_{A_1\times A_2}(x_1,x_2)f_1(x_1)f_2(x_2) \, dx_1 \, dx_2\\ &= \mu(A_1\times A_2)\end{align}.$

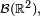
On remarque alors que $\scriptstyle\ \mathcal{C}\$ est un π-système et que la tribu engendrée par $\scriptstyle\ \mathcal{C}\$ est $\scriptstyle\ \mathcal{B}(\R^2),\$ donc, en vertu du lemme d'unicité des mesures de probabilités,

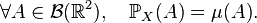
$\forall A\in \mathcal{B}(\R^2),\quad \mathbb{P}_{X}(A)=\mu(A).$

Cas des variables discrètes

Dans le cas des variables discrètes, un critère d'indépendance utile est le suivant :

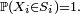
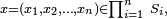
Cas discret — Soit X=(X₁, X₂, ... , X_n ) une suite de variables aléatoires discrètes, et soit (S₁, S₂, ... , S_n ) une suite d'ensembles finis ou dénombrables tels que, pour tout i≤n, $\scriptstyle\ \mathbb{P}(X_i\in S_i)=1.\$ Alors la famille (X₁, X₂, ... , X_n ) est une suite de variables aléatoires indépendantes si, pour tout $\scriptstyle\ x=(x_1,x_2, \dots, x_n)\in \prod_{i=1}^n\,S_i,\$

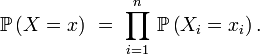
$\mathbb{P}\left(X= x\right)\ =\ \prod_{i=1}^n\,\mathbb{P}\left(X_i= x_i\right).$

Loi uniforme sur un produit cartésien :

Soit (E₁, E₂, ... , E_n) une suite d'ensembles finis, de cardinaux respectifs #E_i , et soit X=(X₁, X₂, ... , X_n ) une variable aléatoire uniforme à valeurs dans le produit cartésien :

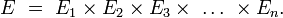
$E\ =\ E_1\times E_2\times E_3\times\ \dots\ \times E_n.$

Alors la suite X est une suite de variables aléatoires indépendantes, et, pour chaque i, la variable aléatoire X_i suit la loi uniforme sur E_i . En effet, considérons une suite Y=(Y_i )_1≤i≤n de variables aléatoires indépendantes, chaque Y_i étant uniforme sur l'ensemble E_i correspondant. Alors, pour tout élément x=(x₁, x₂, ... , x_n ) de E,

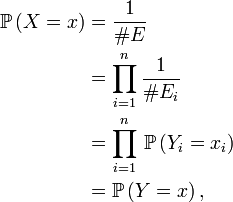
$\begin{align}\mathbb{P}\left(X= x\right)&=\frac1{\# E}\\ &=\prod_{i=1}^n\frac1{\# E_i}\\ &=\prod_{i=1}^n\,\mathbb{P}\left(Y_i= x_i\right)\\ &= \mathbb{P}\left(Y= x\right),\end{align}$

la deuxième égalité résultant de la formule donnant le nombre d'éléments d'un produit cartésien d'ensembles, la 4ème de l'indépendance des Y_i , les autres égalités résultant de la définition de la loi uniforme. Ainsi les suites X et Y ont même loi, ce qui entraîne bien que X est une suite de variables aléatoires indépendantes dont les composantes suivent des lois uniformes.

Une application de ce critère est l'indépendance des composantes du code de Lehmer d'une permutation, qui permet d'obtenir simplement la fonction génératrice des nombres de Stirling de première espèce.
Un autre application est l'indépendance des chiffres du développement décimal d'un nombre uniforme dans l'intervalle [0,1].

Autres critères d'indépendance

Par exemple,

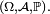
Critères — Soit X et Y deux variables aléatoires réelles définies sur un espace probabilisé $\scriptstyle\ (\Omega,\mathcal{A},\mathbb{P}).\$

Si, pour tout couple (x,y) de nombres réels,

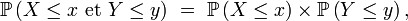
$\mathbb{P}\left(X\le x\text{ et }Y\le y\right)\ =\ \mathbb{P}\left(X\le x\right)\times\mathbb{P}\left(Y\le y\right),$

alors X et Y sont indépendantes.

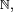
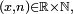
Si Y est à valeurs dans $\scriptstyle\ \mathbb{N},\$ et si, pour tout couple $\scriptstyle\ (x,n)\in\mathbb{R}\times\mathbb{N},\$

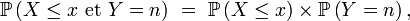
$\mathbb{P}\left(X\le x\text{ et }Y=n\right)\ =\ \mathbb{P}\left(X\le x\right)\times\mathbb{P}\left(Y=n\right),$

alors X et Y sont indépendantes.

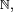
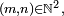
Bien sûr, si X et Y sont à valeurs dans $\scriptstyle\ \mathbb{N},\$ et si, pour tout couple $\scriptstyle\ (m,n)\in\mathbb{N}^2,\$

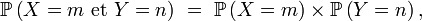
$\mathbb{P}\left(X=m\text{ et }Y=n\right)\ =\ \mathbb{P}\left(X=m\right)\times\mathbb{P}\left(Y=n\right),$

alors X et Y sont indépendantes.

Par exemple, on peut utiliser le deuxième critère pour démontrer que dans la méthode de rejet, le nombre d'itérations est indépendant de l'objet aléatoire (souvent un nombre aléatoire) engendré au terme de ces itérations.

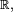
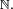
On peut généraliser ces critères d'indépendance à des familles finies quelconques de variables aléatoires réelles, dont certaines, éventuellement, sont des variables discrètes, à valeurs dans des parties finies ou dénombrables de $\scriptstyle\ \mathbb{R},\$ éventuellement différentes de $\scriptstyle\ \mathbb{N}.\$ La démonstration de ces critères se trouve à la page "Lemme de classe monotone".

Indépendance et corrélation

L'indépendance implique que la covariance, et donc la corrélation, entre les deux variables est nulle:

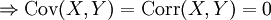
Théorème — X et Y sont indépendantes $\Rightarrow \operatorname{Cov}(X,Y)=\operatorname{Corr}(X,Y)=0$

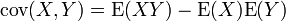
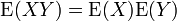
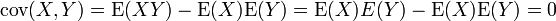
Cette propriété se déduit très facilement si l'on exprime la covariance comme: $\operatorname{cov}(X, Y) = \operatorname{E}(X Y) - \operatorname{E}(X)\operatorname{E}(Y)$ . Comme on l'a vu, l'indépendance de X et Y entraîne que $\operatorname{E}(X Y)= \operatorname{E}(X)\operatorname{E}(Y)$ , donc $\operatorname{cov}(X, Y) = \operatorname{E}(X Y) - \operatorname{E}(X)\operatorname{E}(Y)=\operatorname{E}(X)E(Y)-\operatorname{E}(X)\operatorname{E}(Y)=0$ .

La réciproque du théorème est fausse, comme le montre l'exemple suivant:

Exemple :

Cet exemple est tiré de Ross (2004, p. 306)

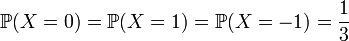
Soit X une variable aléatoire discrète telle que $\mathbb{P}(X=0)=\mathbb{P}(X=1)=\mathbb{P}(X=-1)=\frac{1}{3}$ .

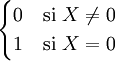
Définissons Y en relation avec X : $\begin{cases} 0 & \text{si } X\neq 0\\ 1 & \text{si } X= 0\\ \end{cases}$

On calcule $\operatorname{E}[XY]= \frac{1}{3}(0\cdot 1)+\frac{1}{3}(1\cdot 0)+\frac{1}{3}(-1\cdot 0)=0$ .

On voit aussi que $\operatorname{E}[X]= \frac{1}{3}(0)+\frac{1}{3}(1)+\frac{1}{3}(-1)=0+1-1=0$ .

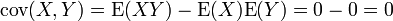
donc: $\operatorname{cov}(X, Y) = \operatorname{E}(X Y) - \operatorname{E}(X)\operatorname{E}(Y)=0-0=0$ .

Pourtant les deux variables ne sont bien évidemment pas indépendantes!

La non-corrélation entre X et Y est une propriété plus faible que l'indépendance. En fait l'indépendance entre X et Y est équivalente à la non-corrélation de φ(X) et de ψ(Y) pour tout choix de φ et de ψ (tels que la covariance de φ(X) avec ψ(Y) soit définie ...).

Indépendance de n évènements

Invention d'un écran à points quantiques étirable

Il y a 6 heures

Un escalator sous l'océan

Il y a 6 heures

Découverte: ces deux vies ont fusionné, accélérant considérablement l'évolution

Il y a 11 heures

Attention, ces additifs alimentaires engendrent un diabète de type 2

Il y a 11 heures

Des traitements anti-VIH pourraient combattre la maladie d'Alzheimer

Il y a 13 heures

Quelle est la différence entre sport et activité physique ?

Il y a 13 heures

Grande avancée sur la compréhension de l'origine des tumeurs

Il y a 1 jour

La malbouffe consommée à l'adolescence a des impacts irréversibles sur la mémoire

Il y a 1 jour

Batteries: capacité triplée avec ces nouvelles anodes en silicium !

Il y a 1 jour

La moelle épinière possède sa propre mémoire

Il y a 1 jour

Cette équation prédit une "magnetic RAM" un million de fois plus rapide

Il y a 1 jour

Des humains ont vécu dans cet immense tube de lave il y a 7000 ans

Il y a 1 jour

L'anxiété et la dépression peuvent diminuer grâce à cette stimulation transcrânienne

Il y a 2 jours

Le bon ratio oméga-6/oméga-3 dans l'assiette pour lutter contre l'obésité

Il y a 2 jours

Des particules plus rapides que la lumière ? Premier test réussi pour les tachyons

Il y a 2 jours

Cette nouvelle approche permet de cibler les cellules cancéreuses pour les combattre

Il y a 2 jours

Intel dévoile le plus grand ordinateur neuromorphique au monde, imitant le cerveau humain

Il y a 2 jours

Cette créature expliquerait notre réaction instinctive de combat ou de fuite

Il y a 2 jours

Les traumatismes de l'enfance altèrent les fonctions musculaires en vieillissant

Il y a 3 jours

Pourquoi nous gratouillons-nous si souvent pour rien ?

Il y a 3 jours

Découverte d'un serpent géant, le plus grand de tous les temps ?

Il y a 3 jours

Découverte d'un nouveau principe de mouvement dans les cristaux liquides

Il y a 3 jours

Une concentration extrême de matière noire révélée par cet anneau d'Einstein

Il y a 3 jours

Comment les émissions des véhicules à essence se transforment en particules respirables

Il y a 3 jours

L'atmosphère de Vénus fuit dans l'espace

Il y a 4 jours

Quand la lutte contre la pollution de l'air contribue au réchauffement climatique: le paradoxe environnemental

Il y a 4 jours

Un trou noir dormant géant découvert dans notre voisinage cosmique

Il y a 4 jours

Grippe aviaire: le risque de propagation aux humains "extrêmement préoccupant" d'après l'OMS

Il y a 4 jours

Le secret des crânes coniques et des dents limées des Vikings

Il y a 4 jours

Les terres rares, loin d'être rares, affectent les plantes

Il y a 4 jours

La marine américaine développe sa première arme à micro-ondes contre les drones

Il y a 5 jours

Premier atlas de l'ovaire humain: un pas vers l'ovaire artificiel

Il y a 5 jours

La vision suffit pour produire les mouvements collectifs (vidéo)

Il y a 5 jours

Comment la Voie lactée a-t-elle influencé l'Egypte antique ?

Il y a 5 jours

Coopérer ou rivaliser: comment décide notre cerveau ?

Il y a 5 jours

S'inspirer des os de géants pour la construction

Il y a 6 jours

Rigidité artérielle: un nouvel indicateur pour prévenir les maladies cardiovasculaires

Il y a 6 jours

Pourquoi les femmes seules consomment-elles plus de sucreries ?

Il y a 6 jours

Que faut-il savoir sur les PFAS, ces "polluants éternels" ?

Il y a 6 jours

Découverte: ces substances courantes accélèrent le vieillissement

Il y a 7 jours

Des scientifiques identifient le meilleur moment de la journée pour faire du sport

Il y a 7 jours

Cette rupture technologique pourrait décupler la capacité des disques durs

Il y a 7 jours

Cycle menstruel: une étude scientifique établit un lien avec la Lune

Il y a 7 jours

Quand un trio d'étoiles devient un couple: une histoire cataclysmique retracée

Il y a 7 jours

Ce petit ver possède des yeux immenses: pourquoi ?

Il y a 7 jours

D'où vient cette structure fractale observée dans une bactérie ?

Il y a 8 jours

Découverte majeure dans les allergies respiratoires

Il y a 8 jours

Voici ce qui a produit la lumière la plus lumineuse jamais détectée dans l'Univers

Il y a 8 jours

Propagation inquiétante de la "mouche noire" suceuse de sang en Allemagne

Il y a 8 jours

Le hasard confère le prix Turing et 1 million de dollars au mathématicien Avi Wigderson

Il y a 8 jours

Populaires

Découverte d'un serpent géant, le plus grand de tous les temps ?

Invention d'un écran à points quantiques étirable

Des particules plus rapides que la lumière ? Premier test réussi pour les tachyons

Un escalator sous l'océan

Découverte: ces deux vies ont fusionné, accélérant considérablement l'évolution

Quelle est la différence entre sport et activité physique ?

Toutes les ventes flash et Codes Promos Amazon

Cdiscount: les meilleures réductions actuelles

Page générée en 4.209 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise