Inconnue (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Une inconnue, en mathématiques, est un élément constitutif d'une question de même nature qu'une équation. L'inconnue permet de décrire une propriété vérifiée par une ou plusieurs valeurs qui prendraient la place de cette inconnue, ces valeurs étant souvent des nombres. Dans le cas d'une équation, une bonne réponse est une valeur pour laquelle, quand on la substitue à l'inconnue, l'égalité est vérifiée. Cette réponse prend le nom de solution. L'inconnue est aussi utilisée dans d'autres situations comme une inéquation. Un problème peut comporter plusieurs inconnues, mais chacune d'entre elles est exprimée sous la forme d'un seul et unique symbole.
Une inconnue possède les mêmes propriétés algébriques, que les objets mathématiques susceptibles de lui être substitués. Il est ainsi possible d'additionner x avec x, on obtient 2x. D'une manière générale, les opérations applicables aux valeurs possibles de l'inconnue le sont aussi à celle-ci. C'est quand on opère ainsi que l'on parle vraiment d'inconnue au sens mathématique. Mais l'inconnue peut juste désigner une valeur que l'on cherche à expliciter sans qu'elle soit véritablement utilisée pour modéliser la question.
Historiquement, l'inconnue est d'abord utilisée dans la modélisation de problèmes de nature algébrique, qui mettent en jeu des polynômes. Ce cas particulier correspond à une théorie qui était appelée théorie des équations. Mais ce cadre s'est élargi : avec en particulier les progrès de l'analyse apparaissent des équations traitant d'autres fonctions que les fonctions polynomiales, et l'inconnue n'est plus forcément un nombre mais, par exemple, un vecteur ou une fonction.
Si le terme inconnue apparaît sous la plume de Pierre de Fermat, un mathématicien du XVIIe siècle, le concept est plus ancien. Diophante au IIIe siècle introduit l'arithme, qui bien que moins opératoire, préfigure l'inconnue moderne. Le vocabulaire et certains principes fondamentaux de la résolution des équations, comme celui de la balance, proviennent en grande partie du mathématicien Al-Khawarizmi et de ses disciples.
Exemples introductifs
Exemple du premier degré
Un exemple de question introduisant une inconnue est :
Question — Un tas et son cinquième, cela fait 21. Quel est ce tas?
L'usage d'une inconnue permet de résoudre cette question. Si X désigne le tas, la question se résume à trouver la solution de l'équation suivante :
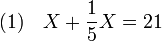
En effet, répondre à la question consiste à trouver une valeur telle que, si l'inconnue X est remplacée par cette valeur, l'égalité est vraie. Ceci montre bien que le problème se formalise par l'équation (1) et la recherche de sa solution. Pour toute valeur, la valeur et son cinquième est égale à 6/5 de la valeur, l'équation (1) peut prendre la forme suivante :
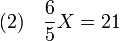
Si deux valeurs sont égales, le produit de chacune des deux valeurs par 5 sont encore égales, il est possible de multiplier les deux membres de l'égalité (2), sans pour autant modifier les solutions des équations associées, et :
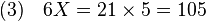
Le même raisonnement montre qu'il est possible de diviser par 6 les deux membres de l'équation (3), sans changer la racines de l'équation associée. On obtient X = 105/6 = 35/2 = 17+1/2. La valeur de la solution est explicitée, le tas est égal à 17+1/2.
L'équation (1) se compose, pour chacun des deux membres de l'égalité, d'une somme de termes formés, soit d'un produit d'un nombre et de l'inconnue, soit d'un nombre. Ce type d'équation est dite du premier degré.
Cet exemple met en valeur deux propriétés de l'inconnue et de l'équation qui l'utilise. La première traite des propriétés algébriques de l'inconnue. Le passage de l'égalité (1) à la (2) est obtenue à l'aide d'une factorisation, une somme de deux termes X + 1/5.X est égale à un produit 6/5.X. Il est possible d'additionner deux termes contenant une inconnue exactement comme si l'inconnue était un nombre. De même, il est possible de multiplier l'inconnue par 5 et de la diviser par 6, ou encore de la multiplier par 5/6. On peut additionner et multiplier des termes contenant l'inconnue, par un nombre ou encore par une expression contenant l'inconnue. Ces facultés sont appelées propriétés algébriques de l'inconnue car elles traitent de son comportement vis à vis des opérations somme et produit.
La deuxième propriété est parfois appelée le principe de la balance. L'égalité définissant l'équation peut être vue comme deux plateaux d'une balance, si les valeurs sont assimilées à des poids. L'égalité est vérifiée si les poids, à droite et à gauche du signe égal, sont les mêmes. Si tel est le cas, on peut ajouter, retrancher, multiplier ou diviser les poids de la même manière à droite et à gauche sans modifier l'équilibre. On utilise ce principe pour passer de l'égalité (2) à la (3), on multiplie par 5 de chaque côté de l'égalité.
Exemple du deuxième degré
L'inconnue permet de résoudre des problèmes plus difficiles. L'exemple choisi ici est dit du second degré :
Question — Un champ rectangulaire possède une aire de 96 et un périmètre de 40. Quelles sont les longueur et largeur du champ?
Dans un premier temps, l'objectif est de traduire la question posée en une équation. Comme le périmètre est égal à 40, la somme de la longueur et de la largeur est égale à 20. On considère la demi-somme c'est-à-dire 10. L'inconnue choisie ici, notée X, représente la valeur à ajouter à 10 pour obtenir la longueur, par définition égale à 10 + X. La somme de la longueur et de la largeur est égale à 20, ce qui signifie que la largeur est égale à 10 - X. Dire que l'aire est égale à 96 revient à dire que le produit de la longueur et de la largeur est égal à 96, ce qui permet de construire l'équation répondant à la question :
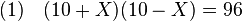
Dans un deuxième temps, on applique des transformations à l'équation de telle manière à rendre visible la ou les valeurs possible(s) de X pour l'instant cachée(s) dans l'équation. Ces valeurs, que l'on rend visible, sont aussi appelées racines. Une identité remarquable est vraie pour tout couple de nombres, elle est aussi applicable à une expression contenant une inconnue :
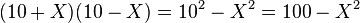
Cette identité remarquable permet d'écrire différemment l'équation (1) :
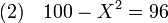
Ajouter X2 - 96 à chacun des deux membres de l'égalité ne modifie pas les solutions de l'équation :
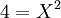
Comme la longueur est plus grande que la largeur, X est nécessairement positif, la seule solution acceptable est 2.
Dans un troisième temps, on explicite la solution et on vérifie qu'elle est exacte. La longueur est égal à 10 + 2, soit 12 et la largeur à 10 - 2, soit 8. La somme de la longueur et de la largeur est bien égale à 20 et le périmètre à 40. Le produit de la longueur et de la largeur vaut 8 x 12 soit 96, on trouve bien l'aire recherchée. L'usage d'une inconnue permet de résoudre la question.
Cet exemple offre un double enseignement sur l'usage de l'inconnue pour la résolution d'une question. Une démarche possible se déroule en trois temps. En premier lieu, la question posée est traduite sous forme d'équation, comportant par définition une inconnue. Ensuite, une série de transformations dites algébriques rendent visibles la racine, initialement cachée dans l'équation. Ces transformations ont pour but d'isoler l'inconnue dans un des côtés de l'égalité définissant l'équation. Les identités remarquables sont fort utiles pour parvenir à cette isolation. Enfin, on vérifie que la solution trouvée est bien la réponse à la question posée.

















































