Inconnue (mathématiques) - Définition

L'inconnue des algébristes

Définition

Les équations polynômiales (à une inconnue) s'écrivent comme des égalités entre termes n'utilisant comme opérations que l'addition et la multiplication sur une inconnue et des nombres déterminés . Il est toujours possible de les écrire comme l'égalité à 0 d'un terme, appelé polynôme, qui est une somme de produits d’un nombre et d’une puissance de l'inconnue. Les équations des exemples introductifs sont des équations polynômiales.

La résolution des équations polynomiales, ou algébriques, a joué un rôle important dans la naissance et le développement de l'algèbre. La branche des mathématiques traitant de ces cas s'appelait théorie des équations.

Inconnue auxiliaire

On cherche à trouver une valeur x tel que :

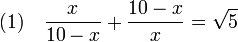
Cette équation se traduit en une équation algébrique en multipliant par x et 10 - x (x doit être différent de 0 et de 10 pour que l'équation initiale est un sens).

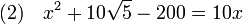
C'est une équation du second degré que l'on peut résoudre directement. Abu Kamil, un algébriste arabe du début du 10ème siècle, à l'idée d'une solution plus simple en choisissant une inconnue auxiliaire. Traduit en termes modernes (Abu Kamil ne dispose pas de notre langage symbolique), il définit y comme représentant (10 - x)/x. L'équation (1) s'écrit maintenant :

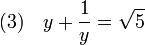
EN multipliant cette équation par y, on obtient une troisième équation :

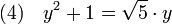
Cette fois-ci, l'équation (4) est de la famille décrite dans la définition précédente. On obtient :

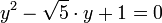
puis

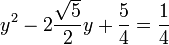
Le membre de droite est une identité remarquable. Avec le formalisme utilisé, on peut écrire autrement l'équation :

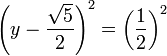
On en déduit deux solutions pour l'équation (3) 1/2(√5 + 1) et 1/2(√5 - 1). L'égalité définissant y, donne, pour chacune des valeurs possibles de y, une équation du premier degré en x. On trouve finalement les solutions 5(√5 - 1) et 5(3 - √5).

Fragments d'histoire

Une préhistoire babylonienne et égyptienne

Aussi loin que remontent les textes mathématiques, on trouve des questions faisant usage du terme inconnue, au sens d'une valeur que l'on recherche et que l'on ne connait pas. La première question introductive de l'article provient d'un vieux papyrus égyptien appelé papyrus Rhind. Dans le texte indiquant comment trouver la solution, inconnue se dit aha et la méthode de résolution utilisée est celle de la fausse position. La deuxième question date des babyloniens, il s'agit encore de valeurs, initialement inconnues et que l'on cherche à établir, connaissant certaines caractéristiques vérifiées par ces dites valeurs. La tablette n'est pas suffisamment explicite pour savoir si la méthode de résolution est géométrique ou non. Les calculs correspondent exactement à ceux présentés dans la solution géométrique et rien ne laisse penser à une formalisation de l'inconnue.

Cette conception de l'inconnue n'est pas considérée par les historiens des sciences comme l'inconnue au sens mathématique du terme. Il désigne ici un mot du langage courant, l'inconnue est ce qui correspond à la question à résoudre et qui devient connue une fois le problème élucidé. Or un formalisme mathématique, associé à la définition même de ce que l'on considère maintenant comme l'algèbre est indispensable pour comprendre l'histoire du concept. A. Dahan-Dalmedico et J. Peiffer précisent : « Le terme d'algèbre, pour une époque où la recherche de l'inconnue n'est pas encore explicite, et encore moins l'étude des "équations", doit être utilisé avec prudence. ». On ne trouve ceci ni dans les mathématiques babyloniennes ou égyptienne, ni dans celles de l'époque d'Euclide chez les grecs.

La méthode de fausse position ou la résolution géométrique de recherche d'un champ d'aire et de périmètre donné, qui ont été présentées plus haut, sont des exemples de méthodes qui n'utilisent pas l'inconnue mathématique, même si elles révèlent bien ce qui était au départ inconnu dans la question posée.

Les travaux de Diophante

Les historiens placent le début du concept d'inconnue, au sens mathématiques du terme, plus de 2.000 ans après la redaction du papyrus Rhind. On le trouve pour la première fois chez un mathématicien du III^e siècle, appelée Diophante.

Son inconnue est appelée arithme, qu'il symbolise par la lettre S : « Le nombre qui possède une quantité indéterminée d’unités s’appelle l’arithme, et sa marque distinctive est S ». Diophante dispose d'un ancêtre de langage symbolique, ainsi Sιβ signifie 12.x car ι symbolise 10, β 2 et S l'inconnue, maintenant notée X. Ce n'est pas tant l'existence d'un langage pré-symbolique qui fait que l'on attribue à Diophante la découverte de l'inconnue au sens mathématique du terme, mais beaucoup plus les propriétés qu'il lui prête.

Dans l'introduction de son livre, intitulé Arithmetica, Diophante précise les règles algébriques, c'est-à-dire qu'il indique comment additionner, soustraire, multiplier et diviser des expressions contenant son arithme : « Ainsi, pour l'arithme, nous dirons l'inverse de l'arithme, pour sa puissance, nous dirons l'inverse du carré » ou encore « L'inverse de l'arithme multiplié par le bicarré de l'arithme donne le cube de l'arithme », ce qui signifie en langage moderne que 1/x multiplié par x⁴ est égal à x³.

Le principe de la balance, c'est-à-dire le fait que l'on puisse ajouter ou retrancher de chaque côté de l'égalité une même expression est développée : « Il est utile que celui qui aborde ce traité se soit exercé à l'addition, à la soustraction et à la multiplication des espèces, ainsi qu'à la manière d'ajouter des espèces positives et négatives avec des coefficients différents à d'autres espèces qui sont elles-mêmes positives, ou même positives et négatives; enfin à la manière de retrancher d'espèces positives et d'autres négatives, d'autres espèces soit positives, soit aussi positives et négatives. Ensuite, s'il résulte d'un problème que certaines expressions sont égales à des expressions identiques, mais avec des coefficients différents, il faudra retrancher de part et d'autre les [espèces] semblables des semblables, jusqu'à ce que l'on obtienne une seule espèce égale à une seule espèce. ».

Ces principes sont les premiers enseignés sur le maniement de l'inconnue, définie au sens mathématique. L. Radfort s'exprime ainsi : « Cette résolution nous permet de voir qu'avec Diophante nous sommes en présence d'un changement conceptuel dans la façon d'aborder certains problèmes mathématiques : une quantité inconnue est mise en scène et cette quantité, l'arithme, va être prise en compte dans les calculs : on va opérer avec elle. »

L'apport de la civilisation arabe

La civilisation arabe s'attache particulièrement à la résolution des équations algébriques. Héritière, à la fois des mathématiques indiennes et grecques, les mathématiciens arabes n'ont pas les mêmes réticences que les hellènes vis à vis des irrationnels. Les mathématiciens indiens travaillent depuis longtemps déjà sur la racine carrée et sur des problèmes du second degré ayant des solutions non rationnelles. Dès le VIII^e siècle les Éléments d'Euclide sont traduits en arabe ainsi que les travaux du mathématicien indien Brahmagupta.

A cette époque, Al-Khawarizmi reprend dans les Éléments d'Euclide la partie traitant de certains problèmes du second degré. Il en modifie profondément l'approche. Le formalisme n'est plus géométrique ni celui d'une question ou d'une liste de questions à résoudre, comme le faisaient les babyloniens ou Diophante, mais la résolution d'une équation, s'exprimant directement avec une inconnue. Son livre Abrégé du calcul par la restauration et la comparaison porte un titre décrivant le principe de la balance déjà décrit : dans une équation, on peut ajouter le même terme des deux côtés de l'égalité, principe appelé al-jabr; ou le retrancher ce qu'il appelle al-muqābala. Ce livre traite de toutes les équations du second degré, on le considère pour cette raison comme : « l'acte de naissance d'une théorie des équations quadratiques, dans l'ensemble des nombres positifs (presque toujours rationnels), théorie qui comporte encore quelques lacunes. »

Par rapport au livre de Diophante, on trouve des régressions, ainsi que des avancées. Le véritable progrès réside dans le fait que la portée de l'inconnue n'est plus limitée aux nombres rationnels, même si les coefficients de l'équation restent presque toujours rationnels. En revanche, Al-Khawarizmi ne développe presque aucun langage symbolique. Son apport essentiel consiste à symboliser l'inconnue par une lettre et à introduire une notation positionnelle des nombres issues des indiens. Cette défaillance n'empêche pas la définition d'un concept rigoureux, mais rend plus complexe le maniement de l'inconnue. De plus, chez Al-Khawarizmi l'inconnue, qu'il appelle shay' et qui signifie la chose que l'on recherche, n'est pas différenciée de la notion de solution, la valeur cachée que l'on recherche, qu'il appelle gizr et qui se traduit en racine.

Ces lacunes sont petit à petit comblées par ses successeurs, Abu Kamil son disciple, généralise l'étude des équations à celles ayant des coefficients rationnels. Al-Karaji développe une arithmétique de l'inconnue, qui préfigure notre algèbre des polynômes. Son œuvre est pousuivie et développée par Al-Samaw'al qui introduit une notation des polynômes comme tableaux de leurs coefficients, bien plus opératoire que celle de ses prédécesseurs. L'écriture symbolique se développe, Al-Karkhi utilise des symboles pour décrire les puissances de l'inconnue, le symbole > placé au-dessus d'un nombre signifie la racine carrée et un signe proche du J désigne le signe égal.

L'apport de la civilisation arabe ne porte pas tant sur la formalisation de l'inconnue, Diophante disposait déjà d'un concept très opérationnel, mais sur son domaine d'application, qui devient ce que l'on appelle maintenant historiquement la théorie des équation, et surtout un environnement syntaxique plus riche, avec une notation décimale et une plus grande richesse de symboles, permettant un maniement plus simple de l'inconnue. L'écriture de l'algèbre en texte reste néanmoins prédominante.

Assimilation européenne

L'Europe découvre les travaux des mathématiciens arabes bien avant ceux de Diophante, au XII^e siècle le texte d'Al-Khawarizmi est traduit en latin par Robert de Chester puis Gérard de Crémone. Certains mots de notre vocabulaire connexes à la notion d'inconnue proviennent de l'arabe. Le terme algèbre est une traduction de al-jabr d'Al-Khawarizmi, le mot racine est une traduction du gizr' du même auteur et, au XVI^e siècle, il finit par fournir les mots racine carrée et radical.

Si le concept de l'inconnue, pour une équation algébrique, est formalisée essentiellement de la même manière en Europe et chez les arabes, le développement d'un langage symbolique plus riche et plus concis, par Viète, Fermat et Descartes, donne une puissance opérationnelle plus vaste et permet d'étendre la théorie des équations.