Inconnue (mathématiques) - Définition

Propriétés

Opérations usuelles

Les deux exemples introductifs illustrent les raisons de la puissance de la méthode. Elle provient du fait qu'il est possible d'opérer sur l'inconnue exactement comme sur une valeur 2, 5 ou √2. Ainsi, la somme de deux multiples de X est le produit de la somme des multiples, par X; par exemple :

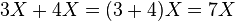
Cette règle est encore valable pour les nombres rationnels ou réels :

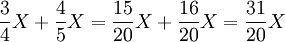
L'associativité de l'addition et de la multiplication est inchangée :

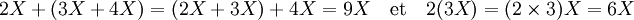
La distributivité de la multiplication sur l'addition est vérifiée sur des expressions contenant une inconnue exactement comme sur les valeurs habituelles :

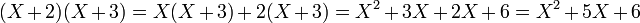
Les puissances d'inconnues suivent les mêmes règles que celles usuelles :

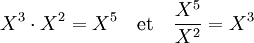
Il est nécessaire d'être un peu prudent avec la dernière égalité. Le terme de droite X⁵/X² n'a pas de sens si X est remplacé par 0. La dernière égalité n'est vraie que si X est remplacé par une valeur différente de 0.

Identité remarquable

certaines identités polynomiales sont appelées « identités remarquables » :

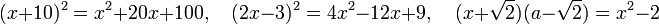
Ces identités sont vraies quelle que soit le nombre que l'on substitue aux variables, ici x. Les équations s'écrivent également comme des égalités, mais qui ne sont en général pas toujours vraies, on cherche justement quelles valeurs substituer à la variable pour que l'égalité soit réalisée. Il est possible d'utiliser une identité pour une variable, jouant éventuellement le rôle d'inconnue dans une équation, ou plus généralement pour toute expression, par exemple polynomiale, utilisant une variable.

Elles sont utiles pour résoudre certaines équations polynomiales, comme celles du second degré. Un exemple est traité dans l'article détaillé, et le cas général dans l'article équation du second degré.

Division par zéro

Une erreur fréquente consiste à diviser deux membres d'une équation par 0, ce qui n'a pas de sens et induit des résultats absurdes. Avec des inconnues, l'erreur est moins flagrante et demande une attention plus soutenue pour l'éviter. Considérons, pour s'en rendre compte, l'égalité entre deux inconnues : X = Y. Cette équation est équivalente aux égalités suivantes :

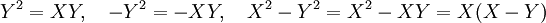
On peut appliquer une identité remarquable à la dernière égalité et, semble-t-il diviser par (X- Y) chaque membre de l'égalité :

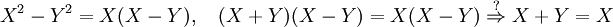
La dernière égalité est étrange, si l'on choisit X égal à 1, Y qui est égal à X est aussi égal à 1 et il semble que l'on a démontré que 2 est égal à 1. L'erreur est commise sur le point d'interrogation, l'implication suppose une division à droite et à gauche de l'égalité par (X- Y). Or comme X est égal à Y, les deux termes sont égaux à 0. Cette division, qui n'a pas de sens, conduit à un résultat absurde.

Cas général

Définition

Les équations algébriques ne permettent pas de résoudre toutes les questions. Il en existe d'autres, soit parce que l'équation s'exprime avec des fonctions qui ne sont pas algébriques, comme le sinus, soit tout simplement parce que la valeur recherchée n'est pas dans un simple ensemble de nombres, comme pour la question que se posait Didon, ou pour l'équation qui régit le mouvement d'une planète autour du soleil, dont l'inconnue est ce mouvement même, et que l'on qualifie de différentielle. Une équation s'écrit plus généralement :

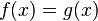
L'inconnue x est une variable, f(x) et g(x) sont des fonctions, elles associent à une valeur, par exemple 1, les nombres notés f(1) et g(1). Si on considère les polynômes comme des fonctions, les équations algébriques s'expriment bien de cette façon. Il est théoriquement possible de mettre toutes les équations sous cette forme, à condition de considérer l'inconnue x comme pouvant appartenir à un ensemble arbitraire (de nombres, de vecteurs, de fonctions, etc.) et les fonctions f et g comme, elles aussi, complètement générales.

Exemple

On cherche à répondre à la question suivante : un coureur se déplace sur une piste circulaire d'un rayon de 100 mètres. Le disque ayant pour frontière la piste, contient une ligne blanche qui parcourt un diamètre, le coureur part d'un point diamètre et de la piste. Quelle distance le coureur a-t-il parcouru la première fois qu'il se trouve à 50 mètres de la ligne blanche ?

La distance parcourue est l'inconnue x de la question, qui se formalise par l'équation suivante :

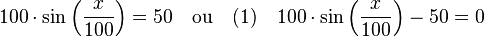
On trouve comme réponse 100.π/6, soit un peu moins de 52,4 mètres. Le terme de gauche de l'équation (1) peut être considéré comme une fonction, qui à x associe la valeur du membre de gauche de l'équation.