Inconnue (mathématiques) - Définition

Première approche

Concept

Le premier sens du mot est associée aux questions comme celle du premier paragraphe : Un tas et son cinquième, cela fait 21. Quel est ce tas ? le terme inconnue désigne la valeur du tas.

La question précédente pourrait s'exprimer sous la forme d'une équation, ce n'est pas toujours le cas : Il y a 5 ans Alice était plus de trois fois plus jeune que Béatrice, qui a maintenant 32 ans. Que sait-on sur l'âge d'Alice ?. L'inconnue est maintenant l'âge d'Alice, répondre à la question revient à dire qu'Alice a entre 5 et 14 ans. L'inconnue se situe donc entre 5 et 14. On voit bien la présence d'une inconnue, mais pas de possibilité de traduire la question sous la forme d'une équation, c'est-à-dire d'une égalité. On parle ici d'inéquation.

L'inconnue n'est pas toujours une valeur, une vieille légende raconte que la reine Didon cherchait à trouver, dans un demi-plan, la surface de périmètre donné et de plus grande aire possible. Cette fois-ci, l'inconnue n'est plus une valeur ou un nombre, mais une figure géométrique, la solution est un demi-disque.

Cette définition, très générale, n'est pas toujours du goût des historiens. Ils considèrent que le terme inconnue, au sens mathématique, s'applique uniquement si l'inconnue dispose d'un minimum de propriétés mathématiques. Ce sens plus précis permet de définir les origines d'une branche des mathématiques appelée algèbre.

Méthode de fausse position

Répondre à la question : Un tas et son cinquième, cela fait 21. Quel est ce tas ?, peut se faire, sans opérer sur une inconnue. La méthode de la fausse position, qui était utilisée dès l'égypte antique, en est une illustration. Elle fonctionne en trois étapes :

• On essaie une première valeur, pour laquelle les calculs sont simples. Si l'inconnue valait 5, le tas et son cinquième vaudrait 5 + 5/5 soit 6. Cette valeur n'est pas celle recherchée.
• On cherche ensuite à appliquer une règle de trois. Par quoi faut-il multiplier 6 pour obtenir 21 ? par 21/6 ou encore 7/2 = 3 + 1/2.
• On multiplie la première valeur essayée, soit 5, par le rapport trouvé dans la règle de trois soit 3 + 1/2. On trouve 15 + 5/2 soit 17 + 1/2. C'est la valeur de l'inconnue recherchée.

Ici, le terme inconnue est synonyme de tas. Il correspond à un terme générique, plus proche de la langue parlée que du concept mathématique.

Résolution géométrique

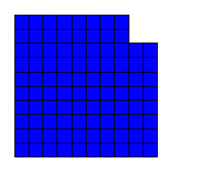
Recherchons maintenant la géométrie d'un rectangle d'aire 96 et de périmètre 40. Si cette surface était un carré, comme son périmètre est 40, son côté serait 10. L'aire est trop grande puisqu'elle vaut 100, au lieu de 96 et elle dépasse de 4. Retranchons au carré d'aire 100, un petit carré d'aire 4 et donc de côté 2. On obtient un gnomon illustré sur figure de gauche.

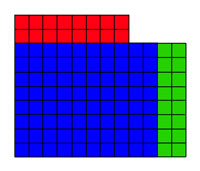
La figure de gauche possède à la fois la bonne aire et le bon périmètre, mais ce n'est pas un rectangle. On considère la bande, illustrée en rouge sur la figure de droite. Elle est exactement de la même dimension que le rectangle vert de la même figure. Retrancher la zone rouge et ajouter la zone verte ne modifie ni le périmètre ni l'aire de la figure.

Le bon rectangle est de longueur 12 et de largeur 8. L'inconnue de la question du deuxième paragraphe est donc 12, correspondant à la longueur d'un rectangle d'aire 96 et de périmètre 40.

Une fois encore, cette méthode a permis de résoudre l'équation sans poser d'équation ni opérer sur une inconnue.