Identité remarquable - Définition

Identités remarquables de degré n

Formule du binôme

La même technique de démonstration que celle utilisé pour les formules de degré 2 montre que, si a et b désignent toujours deux nombres :

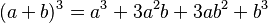
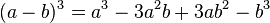
Appliqué encore une fois, on obtient :

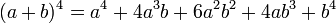
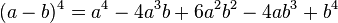
On peut la généraliser à un degré n quelconque, à l'aide de la formule du binôme :

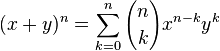
Les coefficients de l'expression, considérée comme un polynôme en x et en y sont appelés coefficients binomiaux. Comme b peut prendre une valeur négative, on obtient bien les deux formes précédentes.

La formule s'applique même si a et b ne sont pas des nombres. Ces lettres peuvent désigner deux matrices qui commutent entre elles. De manière générale, la formule est vraie dans un anneau, si a et b commutent.

Différence ou somme de puissances

Il est aussi possible de généraliser la troisième identité remarquable de degré 2. Si a et b désignent deux nombres :

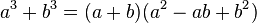
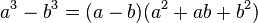
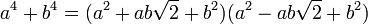
Si l'on travaille dans un ensemble qui n'est pas celui des nombres, la dernière formule n'est valable que si √2 existe, c'est-à-dire s'il existe une valeur c telle que c² soit égal à 1 + 1. Il faut, en conséquence que l'élément neutre de la multiplication existe.

La formule suivante permet de généraliser la démarche :

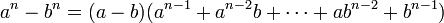
Identités remarquables et arithmétique

Identité de Brahmagupta

Brahmagupta, un mathématicien indien du VI^e siècle découvre une identité remarquable du quatrième degré :

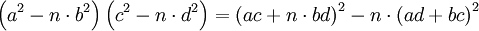
Brahmagupta l'utilise dans le cas où a, b, c, d et n sont des nombres entiers. Elle permet de calculer une bonne approximation d'une racine. Pour calculer √3, il remarque que 2² - 3.1² = 1. Il applique son identité plusieurs fois, toujours avec n = 3. La première fois, il pose a = c = 2, b = d = 1. Il obtient :

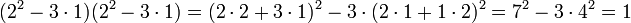
Il recommence avec cette fois avec : a = c = 7, b = d = 4. Il obtient une nouvelle manière d'écrire 1 :

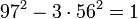
Il réapplique la même logique, il obtient encore une autre manière d'écrire 1:

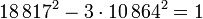
Cette égalité s'écrit encore :

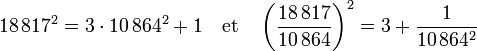
Il obtient une fraction dont le carré est presque égal à 3, ce qui revient à dire que 18 817/10 864 est presque égal à √3. Si on calcule la fraction, on trouve un résultat dont les neuf premiers chiffres significatifs fournissent la meilleure approximation possible (avec le même nombre de décimales), à savoir : 1,73205081. Il utilise aussi sa formule pour trouver des solutions à une équation diophantienne difficile, dite de Pell-Fermat. Sa méthode porte le nom de chakravala.

Identité des quatre carrés d'Euler

L'identité des quatre carrés d'Euler relie entre eux huit nombres. Elle prend la forme suivante :

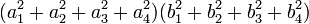
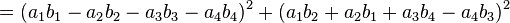
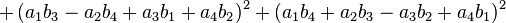
Elle est utilisée, entre autres pour démontrer le théorème des quatre carrés qui indique que tout nombre entier est somme de quatre carrés.